内埋武器系统由于具有低阻力、低可探测性等优点,可以满足新一代战斗机高速飞行及隐身性能的要求而成为首选的武器挂载方式。不同于传统外挂方式,当需要发射武器而开启舱门后,内埋武器舱内部形成强非定常流场,使得弹舱内产生大幅度的压力脉动,造成剧烈震荡并伴随强烈噪声,对武器舱内设备造成破坏[1]。同时剧烈的压力脉动还会改变弹体受力及力矩,引起弹体下落轨迹与姿态角的变化。超声速来流条件下,在弹体出舱后,流场中出现激波相交、激波剪切层反射等一系列复杂流动现象,受其影响弹体表面压力呈现高低压交替分布,弹体受到的气动力产生强烈脉动,威胁武器发射安全,因此针对机弹安全分离的研究也成为热点。Johnson[2]和Davis[3]等通过数值模拟方法及风洞试验发现,受内埋舱强非定常流场的影响,在相同的发射条件下,弹体下落轨迹会随着不同的发射时间而改变。Kim等[4]通过数值模拟发现气帘吹流可以有效抑制舱体流动的非定常性,在一定程度上改善弹体发射条件,有利于弹体安全投放。Westmoreland[5]研究表明弹体投放时施加恰当的弹射力可以显著提升机弹分离品质。Babu等[6]通过数值模拟研究了柔性弹翼和刚性弹翼对弹体下落轨迹的影响。唐上钦等[7]研究了气动干扰对弹体下落的影响,结果表明气动干扰对内埋导弹发射后初始弹道和自控终点纵向、侧向散布影响明显。郭亮等[8]通过在腔体前缘加圆棒扰流器的方法将剪切层向外顶出,使得弹体在下落过程中受剪切层影响延缓并减轻。吴继飞等[9]通过风洞试验方法探究了内埋武器投放的改进措施,发现采用前缘射流进行主动控制能有效提升机弹分离安全性。在文献[10―11]中,对比了弹体内埋投放与外挂投放的区别并探究了舱门的影响,发现内埋投放弹体受到舱门及唇口剪切层强非定常流场的作用,弹体的受力及下落姿态存在较大的波动,威胁内埋弹体的安全分离,但若选取恰当的发射参数则可以大幅度减小舱体内非定常流场对弹体投放的不利影响。因此有必要针对不同发射参数对弹体下落轨迹的影响规律进行深入研究。本文将采用基于 Menter SST湍流模式的改进延迟分离涡模拟(IDDES)方法结合六自由度刚体动力学方程和重叠网格技术对来流马赫数、弹体发射速度、初始角速度等参数对机弹分离品质的影响展开研究,以期为机弹安全分离设计提供借鉴。
1 数值计算方法
1.1 控制方程
本文主要研究弹体投放运动,考虑粘性影响适用于动网格的三维、可压缩、非定常、守恒型控制方程表示如下[12―13]:
式中:W为守恒变量;Fc为对流矢通量;Fv为粘性矢通量;Q为源项;Ω为控制体;Vt为控制体表面的逆变速度;dS为面元。
计算中对流通量采用混合二阶迎风/中心差分格式求解,扩散通量采用中心差分格式。选用具有较小数值耗散的修正Venkatakrishnan[14]限制器,以保证插值精度。非定常计算采用双重时间步法,并应用多重网格技术加速内迭代步收敛。
1.2 IDDES方法
本文湍流模拟采用基于 SSTk- 模型的IDDES方法[15―16]。该方法求解的k和 方程与SSTk-模型方程形式相似,唯一不同的是IDDES模型的k方程中湍动能耗散项Dk计算方式发生了改变,其具体公式如下:
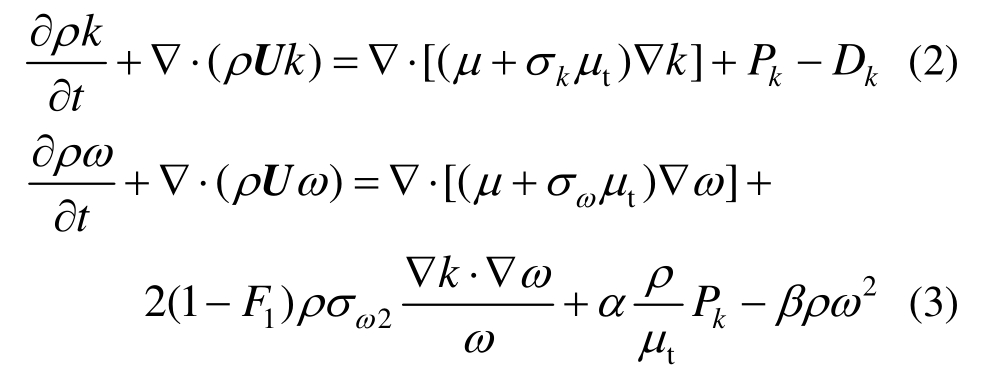
其中: 为密度;k为湍动能;t为时间;U为速度向量; 为分子粘性系数;μt为湍流粘性系数;Pk为湍动能生成项; 为湍流耗散比;β= 0.075;α=α1 F1+α2(1 -F1),其中α1= 5/9,α 2= 0.44;σk=0.85;σω= 0.85;σω 2= 0.856。
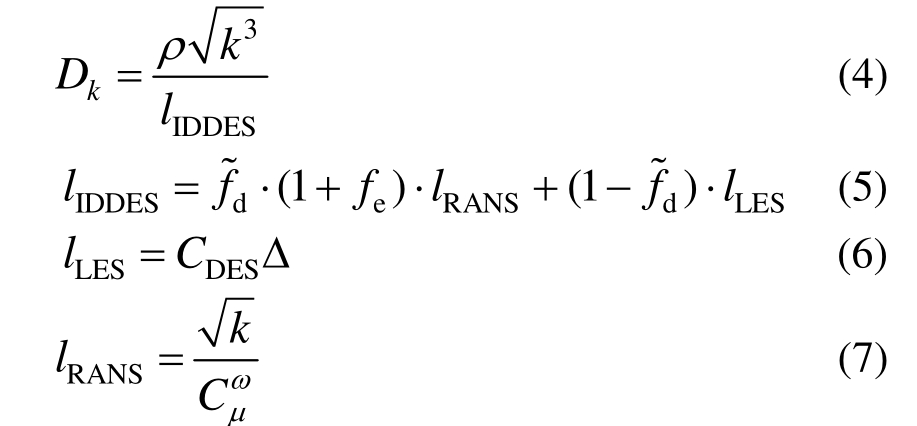
式中:fe和![]() 为插值函数;CDES为比例系数;Cμ= 0.9。由于SST存在k-与k-两个分支,所以比例系数CDES采取两个分支分别较准,然后通过Menter[17]提出的混合函数F1将二者结合起来。
为插值函数;CDES为比例系数;Cμ= 0.9。由于SST存在k-与k-两个分支,所以比例系数CDES采取两个分支分别较准,然后通过Menter[17]提出的混合函数F1将二者结合起来。
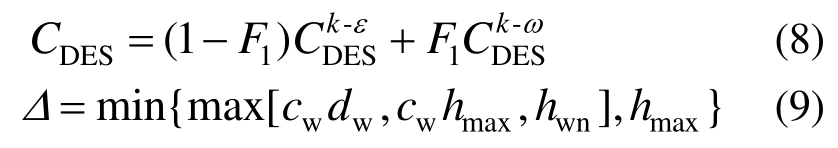
式中:hwn是垂直壁面方向的网格步长;dw为到壁面距离;cw为经验常数,取0.15;hmax为网格三个方向尺寸最大值。
IDDES方法相比于最初版本 DES97[18]及DDES[19]方法,在保留了DES类方法优点的同时成功克服了对数律不匹配、网格诱导分离、模型应力损耗等问题[20]。
1.3 重叠网格法
为了模拟弹体下落,必须采用运动网格技术,现阶段主要有网格变形、网格重构及重叠网格等方法。网格变形方法在处理大尺度位移问题时网格质量会变的很差,甚至有可能相交出现负体积单元,从而导致计算失败。网格重构法可以处理大位移或大变形的问题,但是由于每个时间步都要重新生成网格并进行差值,故而对计算资源需求很高[21―22]。因此本文选用重叠网格方法来实现弹体的运动。
重叠网格法中存在两套或多套相互交叠的网格区域,分别称为背景网格区域和重叠网格区域。在计算中通过将背景网格中被重叠区遮挡的网格隐藏,通常称之为“挖洞”,形成一套计算网格。如果重叠网格区域发生移动,则按一定规则重新进行“挖洞”,来得到新的计算网格,即可实现重叠网格区域的运动。两套网格交界区域的网格被称为插值网格,其作用是将两套网格的解耦合起来。
1.4 六自由度刚体动力学方程
本文选择与机体相连的弹舱为发射惯性坐标系,用来描述弹体质心的运动。弹体运动方程组是描述作用在导弹上的力、力矩与弹体参数之间关系的一组方程,它由描述质心运动和弹体姿态变化的动力学方程、运动学方程和角度几何关系等三类方程组成。

式中:r为弹体质心位移矢量;F为弹体受到的合力;V为弹体质心速度。
式中:M为弹体坐标系下导弹受到的合力矩;ω是弹体角速度矢量;I为惯性矩张量。
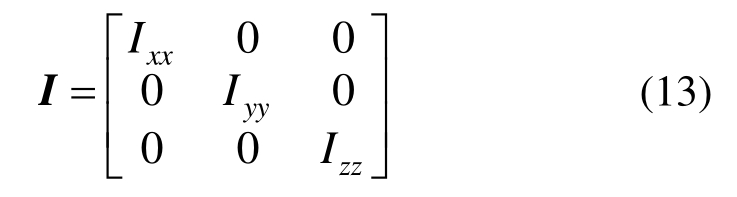
1.5 数值方法验证
机翼/挂架/带舵外挂物模型(Wing/ Pylon/Finned-Store, WPFS)是美国发起的第一次分离投放CFD验证时使用的实验模型,CTS实验测试由Arnold Engineering Development Center(AEDC)完成[23]。本文以该模型实验来验证所选用的数值方法模拟弹体投放过程的准确性。
WPFS模型几何外形如图1所示,机翼根部弦长为7.6 m,半翼展6.6 m,采用NACA64A010翼型,机翼面积为 51 m2。外挂物长 3.39 m,直径0.508 m,弹体质量为907.5 kg,来流马赫数为0.95。模型网格划分为两个区域,包含机翼及挂架的背景网格区域和包含弹体的重叠网格区域。背景网格区域网格总数为 1150万,重叠网格区域网格总数为320万,计算时间步取1×10-3s。
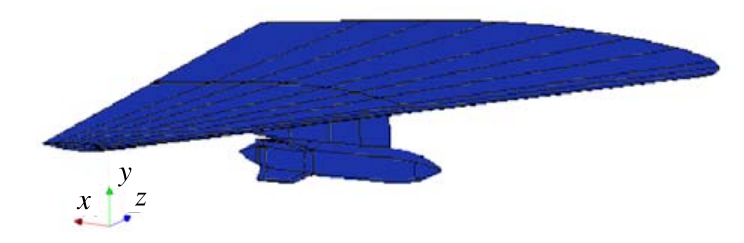
图1 WPFS模型几何外形
Fig.1 Wing/pylon/finned/store geometry
图2(a)为三个方向弹体质心位移随时间变化曲线。从图中可以看出,计算得到的弹体位移变化与实验符合较好,由于弹射力作用,弹体下落方向位移要远大于另外两个方向的位移。图2(b)为弹体滚转、偏航、俯仰姿态角随时间变化曲线,同样由于弹射力作用,在下落初期,弹体俯仰角度增长最快,但撤去弹射力后,在重力和气动力共同作用下俯仰角又开始减小,其余两个方向姿态角一直保持增长趋势。可以看出本文采取的数值方法可以准确地模拟弹体下落运动。

图2 弹体位移及姿态角随时间变化曲线
Fig.2 Displacement and angular orientations of missile versus time curves
2 计算模型和网格划分
2.1 计算模型
如图3所示,本文选取的计算模型为简化的弹舱-舱门-弹体模型,弹舱尺寸为:4.2 m×2 m×0.7 m,弹舱内部形状不规则,底部为弧形。舱门为两段式舱门,第1段内侧有增加强度的凸起肋板,第2段内折。弹体类型为空空导弹,腔体内存在3个弹体挂载位置,本文选取下落环境较为复杂的侧边挂载位置进行研究。弹体长3.27 m,弹径0.18 m,质量170 kg,弹体质心位置距头部尖点 1.84 m,弹体绕x轴的转动惯量Ix=1.37 kg·m2,弹体绕y轴和z轴的转动惯量Iy=Iz=120 kg·m2。
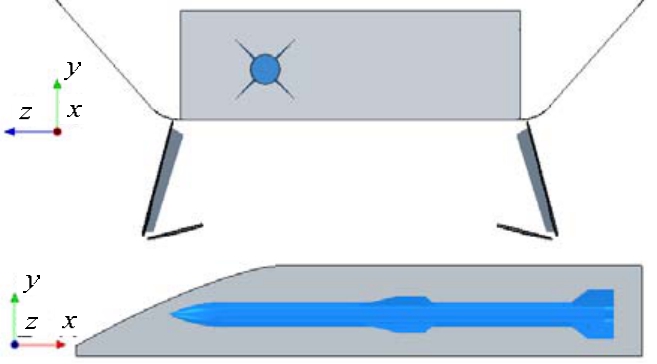
图3 简化计算模型
Fig.3 Simplified simulation model
选择的坐标系为:x轴为逆航向,y轴向上,z轴向左,则按照此坐标系定义,弹体低头为正、左偏航为正。
2.2 网格尺寸选择
划分网格时将弹舱及舱门作为背景网格区域,弹体网格为重叠网格区域。为了保证弹体下落过程中网格挖洞的鲁棒性并保证两套网格间插值具有足够的精度,划分网格时保证两套网格交界处,网格尺寸之比在1.0~1.2。边界层第一层网格尺度设置为2×10-6m以保证y+~1。背景网格数量为2150万,重叠区域网格数目为400万。网格密度分布如图4所示。
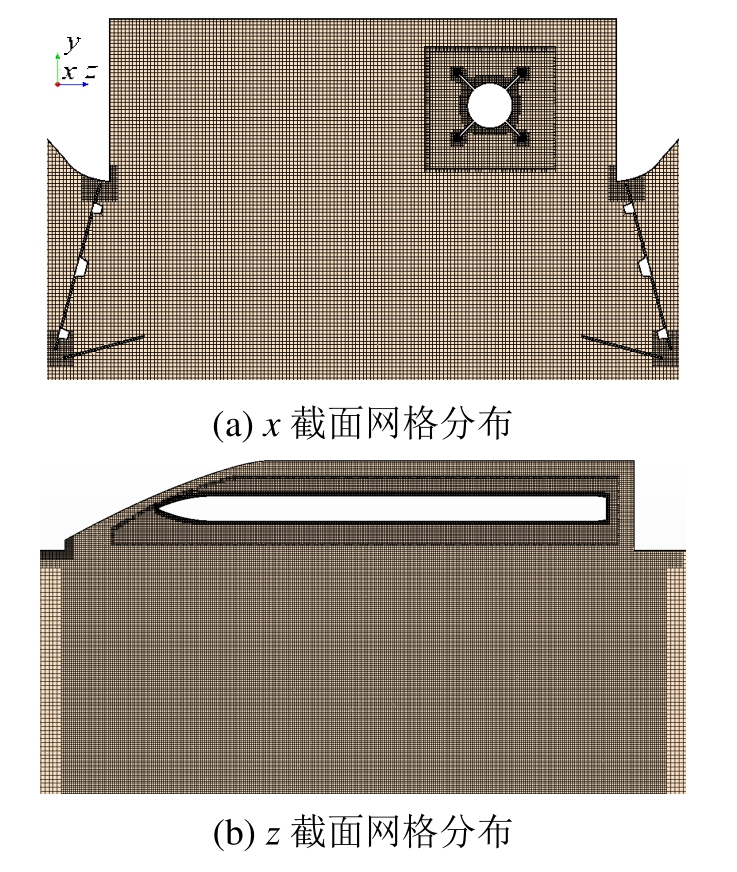
图4 网格密度分布
Fig.4 Grid distribution
2.3 计算条件
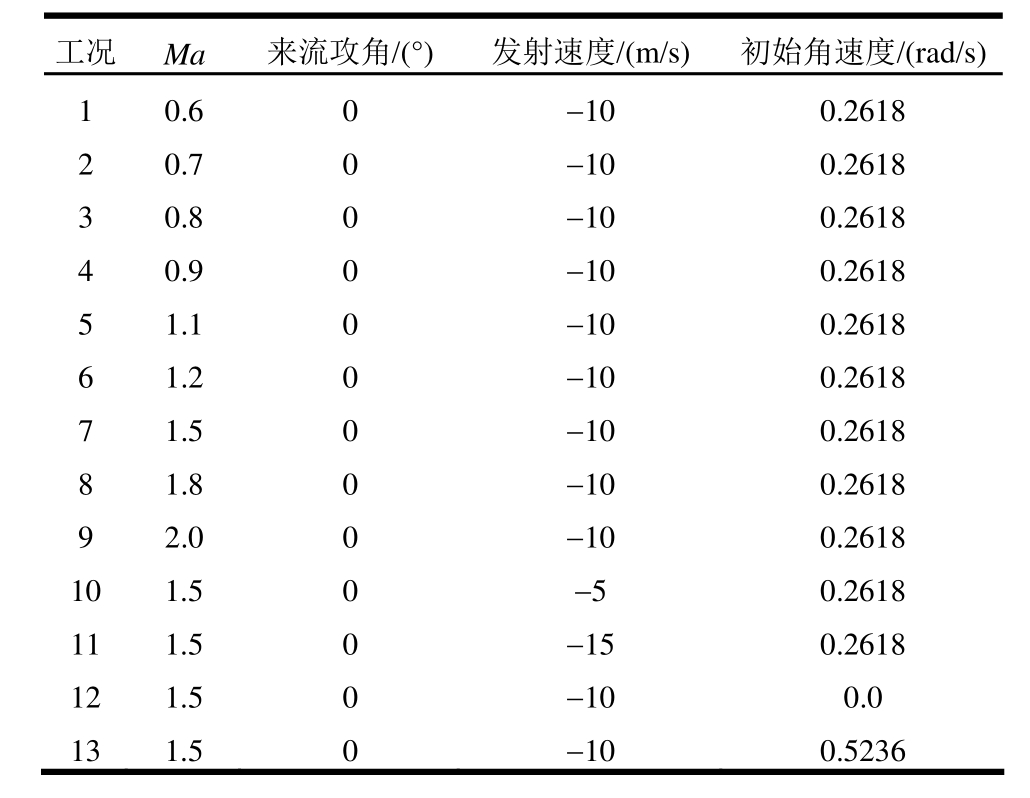
本文研究了不同来流马赫数对弹体下落轨迹的影响,并对Ma=1.5条件下,弹体不同发射速度、角速度等因素对弹体下落轨迹的影响进行了详细分析,具体工况见表 1。本文算例入口条件设置为远场自由来流条件,壁面均采用无滑移壁面条件。计算时间步长为5×10-4s,内迭代步设置为20步,可满足残差下降两个量级。在流场建立之后,又继续进行了0.1 s的非定常计算,在t =0.1 s时弹体开始下落,计算停止准则为弹体下落位移达到3.5 m。
表1 计算工况
Table 1 Simulation cases
3 结果分析
文献[24]给出了机弹分离安全性的定性判别准则,将机弹分离品质分为两种不安全分离及3种安全分离情况。不安全分离:1) 弹体姿态角变化剧烈且在某个方向上有贴近载机的趋势;2) 弹体发射后直接与载机碰撞。3种安全分离为:1) 弹体发射后远离载机,姿态角无明显变化;2) 弹体发射后远离载机,弹体呈现小姿态运动;3) 分离后弹体姿态角变化剧烈,长时间滞留在载机干扰流场内,与载机距离增加缓慢,此分离状态可以接受,但要尽量避免。本文根据此准则评价不同工况弹体分离品质。
3.1 来流马赫数对弹体下落轨迹影响
图5(a)~图5(c)为不同来流马赫数条件下,弹体竖直方向合力、速度及位移随时间变化曲线。图 6(a)~图6(c)为弹体偏航力矩、偏航角速度及偏航角随时间变化曲线。图 7(a)~图 7(c)为弹体俯仰力矩、俯仰角速度及俯仰角随时间变化曲线。图8为弹体姿态角随来流马赫数变化趋势。从图5~图7弹体受力及力矩曲线中得知,投放初期弹体受力和力矩均存在强烈的脉动,随着下落位移的增加,投放后期弹体受力脉动幅度有所降低。这是因为当舱门开启后内埋舱唇口剪切层产生强涡流,流场呈现强非定常特性。受其影响弹体表面压力存在剧烈脉动,致使弹体受力呈现大幅度波动。随着下落距离逐渐增加,弹体远离武器舱,受到舱体附近强涡流场的影响逐渐减小,因此下落后期弹体受力波动幅度降低。
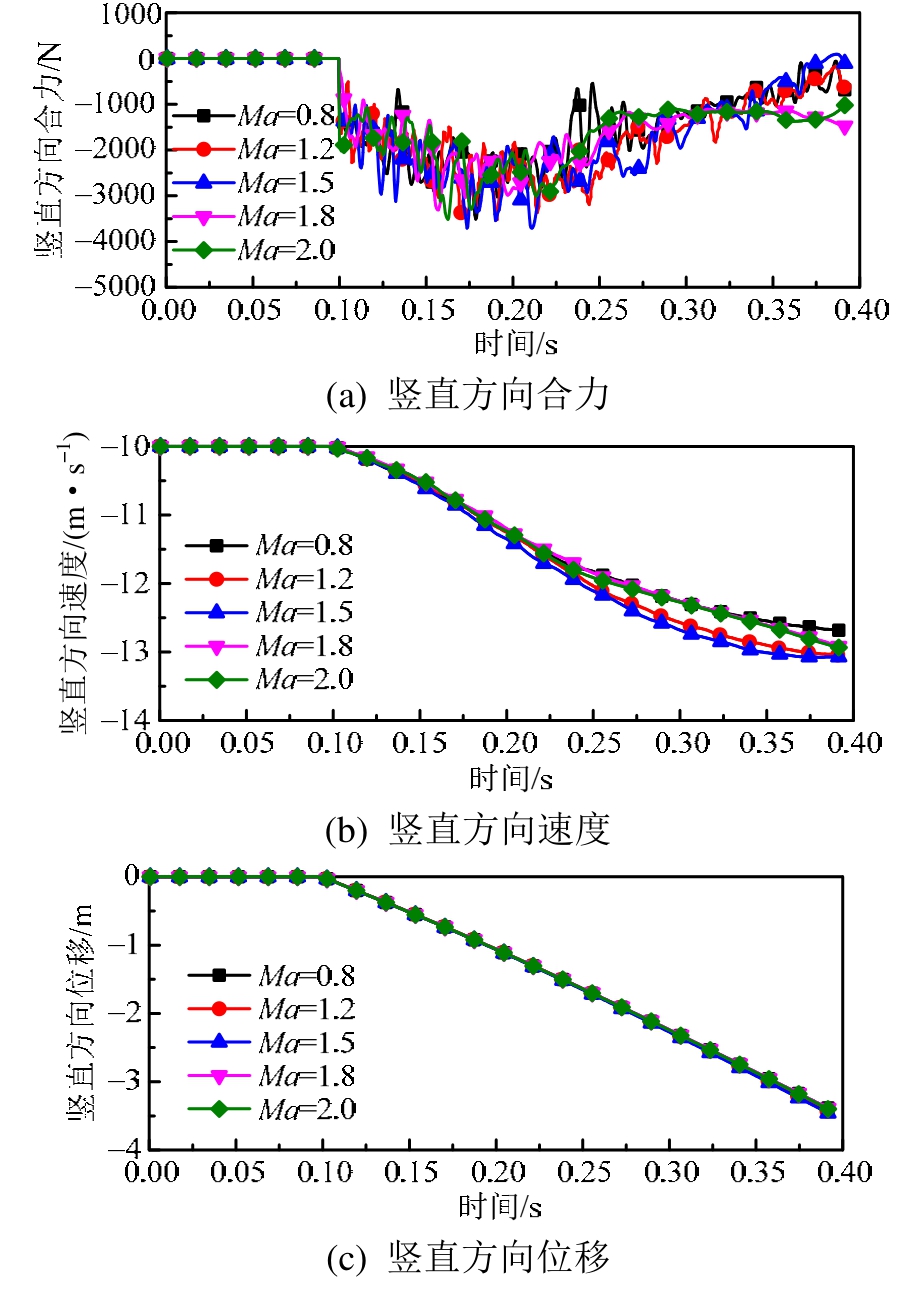
图5 不同马赫数竖直方向合力、速度、位移随时间变化
Fig.5 Vertical force, velocity and displacement of missile versus time curves for different Mach numbers
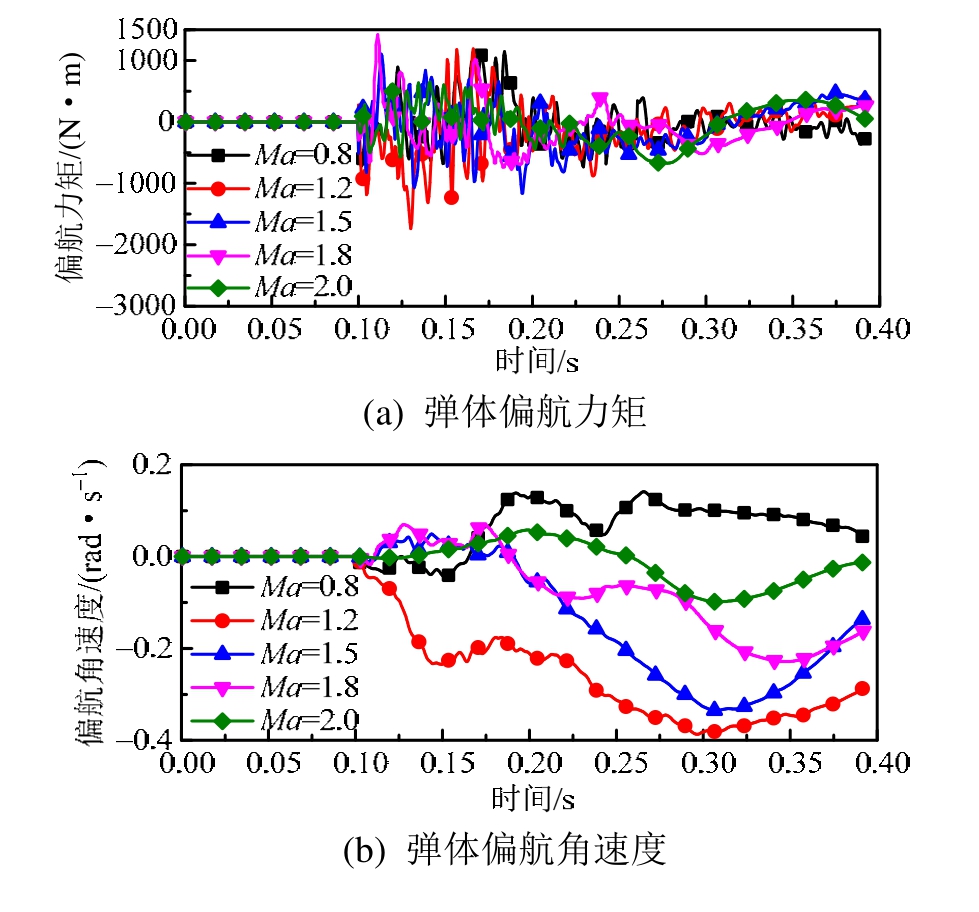
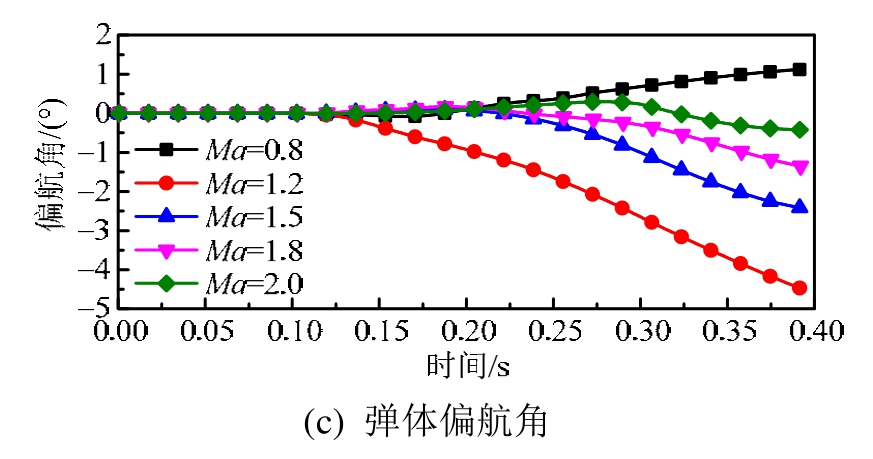
图6 不同马赫数偏航力矩、角速度、偏航角随时间变化
Fig.6 Yaw moment, yaw angular velocity and yaw angle of missile versus time curves for different Mach numbers
图7 不同马赫数俯仰力矩、角速度、俯仰角随时间变化
Fig.7 Pitch moments, pitch angular velocity and pitch angle of missile versus time for different Mach numbers
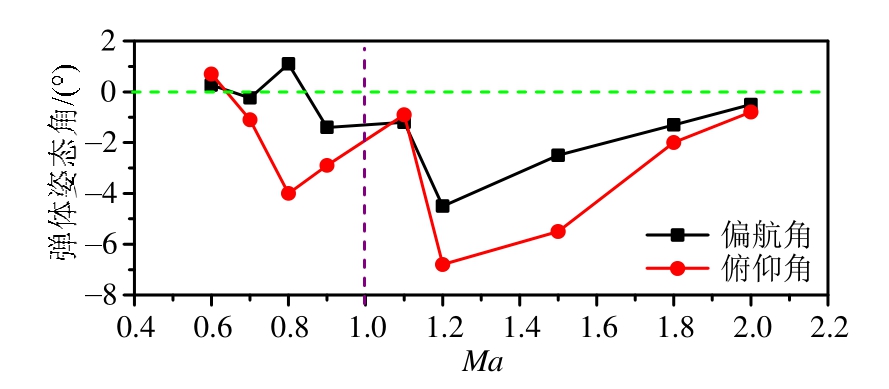
图8 弹体姿态角随来流马赫数变化趋势
Fig.8 Variation trend of angular orientations of missile versus inflow Mach number
从图5可以看出,不同来流马赫数条件下,弹体下落速度差别较小,弹体下落位移曲线基本重合。从图6及图8可知,在亚声速条件下,来流马赫数对弹体偏航角度影响较小,此时由于弹舱-舱门-弹体以及来流之间的发射扰动,使得弹体发生小角度偏航;在跨声速及超声速条件下弹体均向右偏航,工况6中弹体右偏航角最大,幅值为4.5°,此后随着来流马赫数的增加弹体偏航角反而降低。
下面选取Ma=0.8、Ma=1.2和Ma=1.5三种代表性工况,对其流场进行详细分析,来探究不同来流马赫数条件下弹体偏航角出现差异的原因。图9为t=0.175 s流场y截面马赫数分布云图,图10为该截面压力系数分布云图,y截面位置如图11所示,即图中1-1截面。图12为不同工况中,弹体左、右两侧表面对称线压力系数分布,记弹体头部尖点坐标x=0,图中虚线表示弹体质心位置。
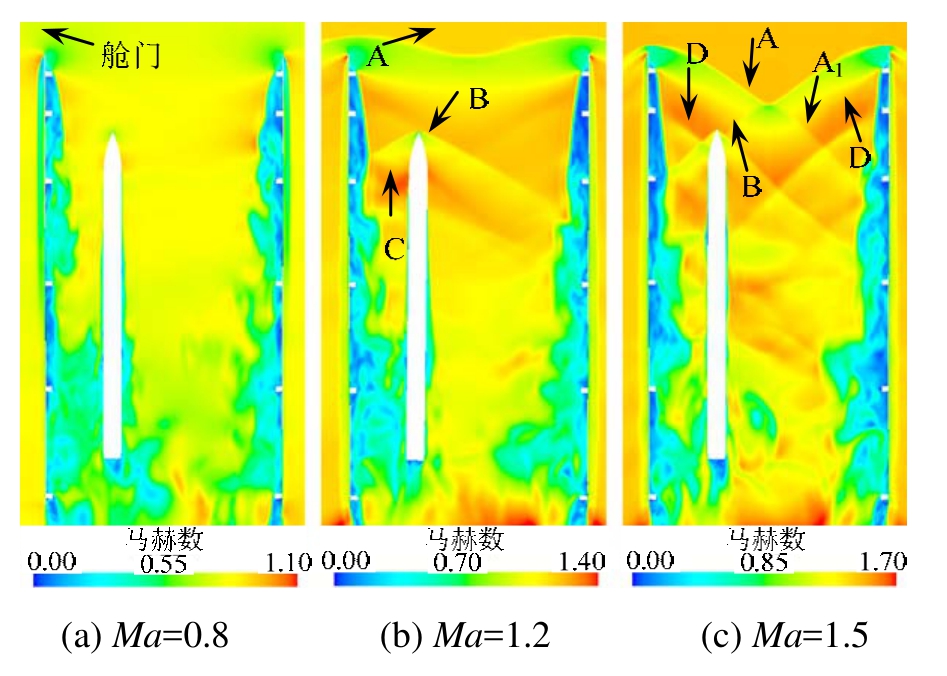
图9t=0.175 s流场y截面马赫数分布云图
Fig.9 Mach number contour ofycross section fort=0.175 s
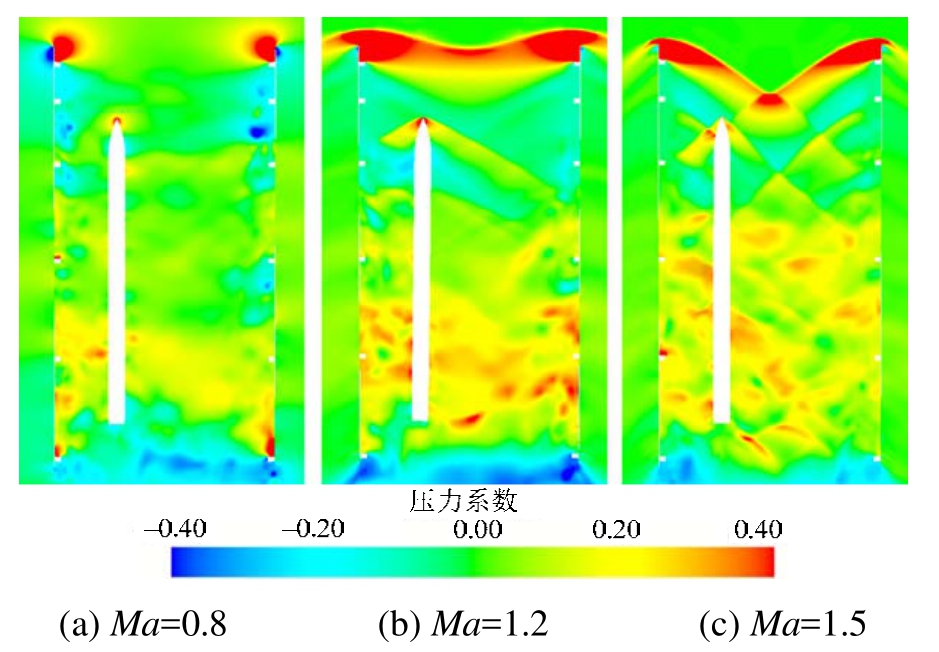
图10t=0.175 s流场y截面压力系数分布云图
Fig.10Cpcontour ofycross section fort=0.175 s
图11 截面位置示意图
Fig.11 Section position
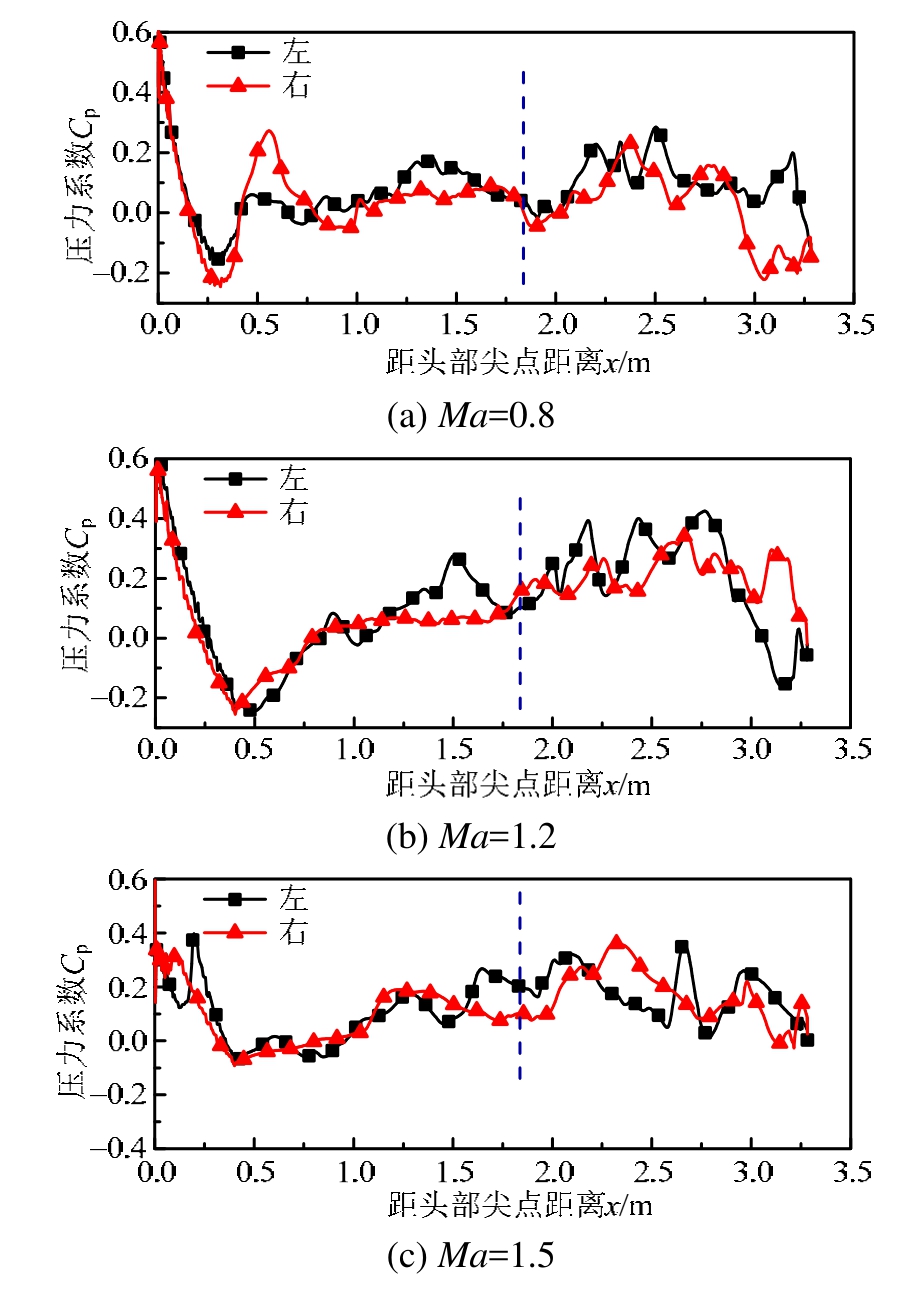
图12 弹体左右两侧对称线压力系数分布曲线
Fig.12Cpdistribution of symmetric line on left and right surfaces
从图9(a)及图10(a)可以看出,工况3流场中无明显的波系结构,弹体两侧流场较为对称,从图 12(a)可以看出弹体左右两侧压力系数分布较为对称,仅在弹体尾部区域差别较大。这是由于弹体挂载点靠近左侧舱门,因此弹体发射时受到舱门附近分离流动的干扰所导致的。工况1及工况2流场与其类似,因此亚声速条件下弹体仅存在小角度偏航,来流马赫数对弹体偏航角影响较小。
工况 6和工况 7为超声速来流,从图 9(b)、图 9(c)可以看出,流场中出现了明显的波系结构,同时还可以发现由于弹体挂载点未在腔体中间位置而是靠近左侧舱门,因此弹体左右两侧波系结构并不对称。工况6中在舱门前端形成斜激波A,两侧舱门引发的斜激波在中心线附近相交,但由于激波强度较弱,无明显透射激波。在弹体头部产生一道斜激波B,受弹体头部形状影响,波后气流持续加速,压力不断降低,为了平衡下游压力又产生了一道斜激波C。由于弹体左侧舱门附近存在分离流的作用,使得激波C强度较高。从图10(b)可以看出,弹体左侧波后压力升高幅度更大,该位置对应于图 12(b)x=1.5 m处,弹体前部左侧压力高于右侧,使弹体产生右偏航力矩。弹体后部流场脉动性较强,压力分布不规则,从两图中还可以看出弹体尾部压力分布与亚声速来流情况相反,右侧压力高于左侧,使弹体产生右偏航力矩,因此Ma=1.2时弹体下落时向右偏航。
工况7来流马赫数由Ma=1.2增加到Ma=1.5,马赫数增加使得舱门前端斜激波 A及弹体头部斜激波B强度增强、马赫角减小。舱门前端斜激波相交后产生透射激波A1,由于马赫角减小,透射激波A1向弹体位置延伸,与弹体头部斜激波B再次发生波系相交,之后作用在弹体头部右表面,图 12(c)中x=0.1 m位置处右侧压力系数升高即为该透射激波引起。流场中还存在新类型斜激波D,弹体左侧激波D与弹体头部激波B发生激波相交,透射激波打在弹体表面,从图12(c)可以观察到x=0.25 m位置处左侧压力系数升高,且比x=0.1 m处升高幅度更大,弹体头部左右两侧压力总体上使其受到较小的右偏航力矩。弹体右方的激波D与透射激波A1及弹体头部斜激波B分别相交后作用于弹体右侧表面,使得该位置弹体右侧表面压力升高。由于受到弹体右侧波系的影响,虽然弹体下落过程中受到的偏航力矩整体上仍为右偏航力矩,但其幅值小于工况 6,因此弹体下落过程中同样向右偏航,但偏航角度较小。
与工况7类似,工况8及工况9中来流马赫数进一步增加,流场中激波强度随之增长,激波角进一步减小,弹体右侧波系的作用增强,使得弹体右偏航力矩持续降低,抑制了弹体右偏航角速度的增长,弹体右偏航角度也随之下降。
从图7及图8可以看出,不同来流马赫数下弹体俯仰角差异也十分明显。当来流马赫数由亚声速增加到超声速后,由于流场中激波的影响,俯仰角度从0.4°变为-6.8°,之后超声速来流条件下随着马赫数增加,弹体俯仰角度随之减小,俯仰角与偏航角变化趋势相似。从图 7(b)可以看出,t =0.1 s~t =0.25 s时间段,各工况中弹体俯仰角速度变化趋势保持相同,然而在t=0.25 s以后,工况8及工况9中弹体俯仰角速度迅速降低。从图7(a)可以看出,此时两种工况弹体俯仰力矩由抬头力矩快速转为低头力矩。下面对t=0.25 s时各工况流场进行分析,探究弹体俯仰力矩发生变化的原因。
图13为t =0.25 s流场z截面马赫数分布云图。从图中可以看出亚声速来流条件下流场中不存在激波,当来流为超声速时,流场中存在舱门前端斜激波A和弹体头部斜激波B。不同马赫数对应的流场中波系结构存在较大区别,马赫数增加引起激波马赫角减小,使激波A向下游移动,与弹体头部距离逐渐缩小。如图所示,当弹体下落到一定距离后,工况8和工况9中,斜激波A与弹体头部激波B发生异族激波相交,生成的透射激波作用在弹体头部,导致头部上表面高压区面积及强度增加,产生很大的低头力矩,因此弹体受到的合力矩由抬头力矩迅速转为低头力矩。与工况8及工况9相比,工况7中来流马赫数较小,斜激波A强度相对较低,同时弹体需要下落到更远的距离,随着距离增加作用在弹体头部的斜激波A强度进一步减弱,因此弹体头部压力升高不如上述两种工况明显。工况6中弹体受到斜激波A的影响最小,下落过程中弹体抬头力矩未受到抑制,因此弹体俯仰角度最大。
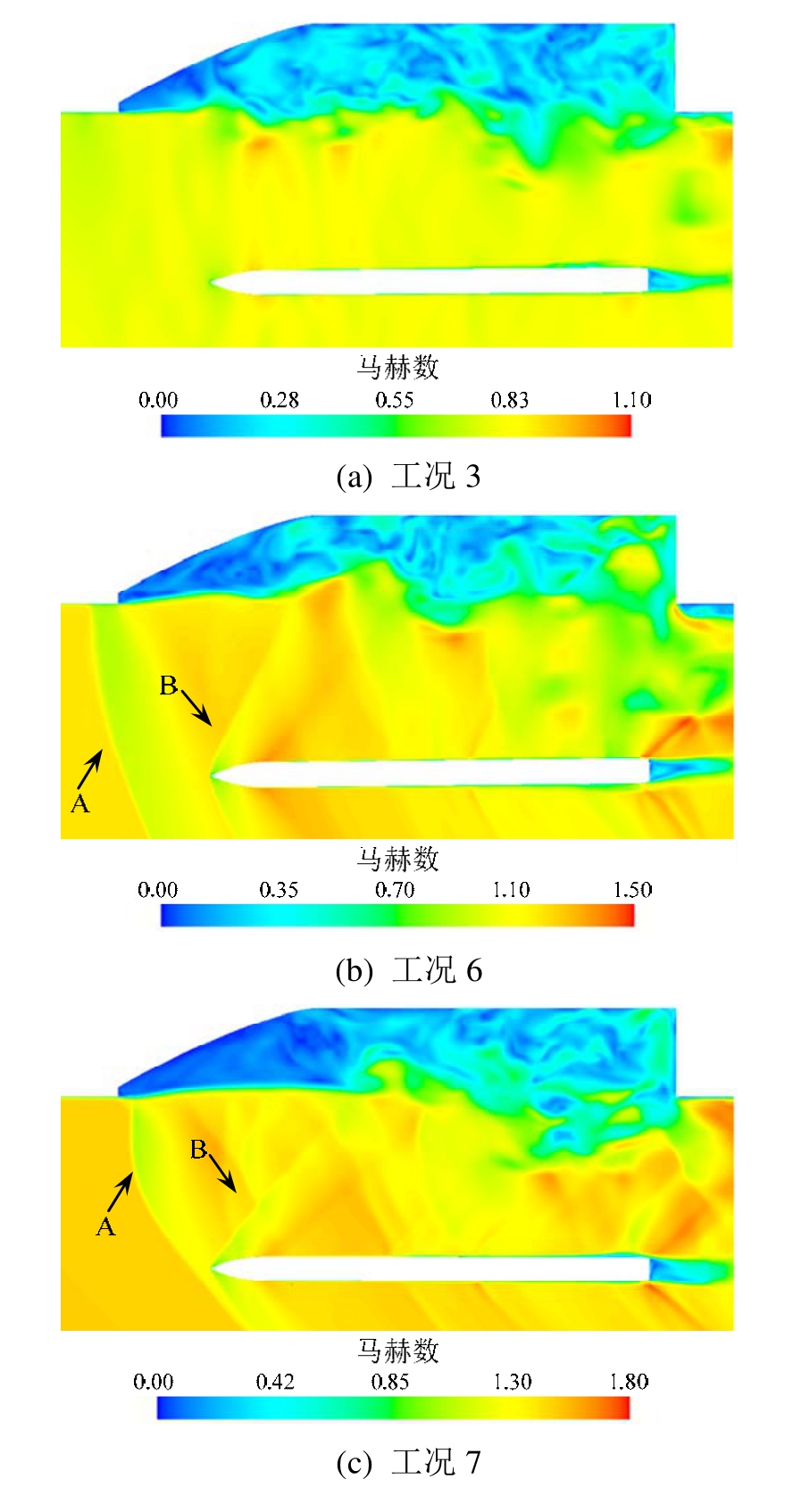
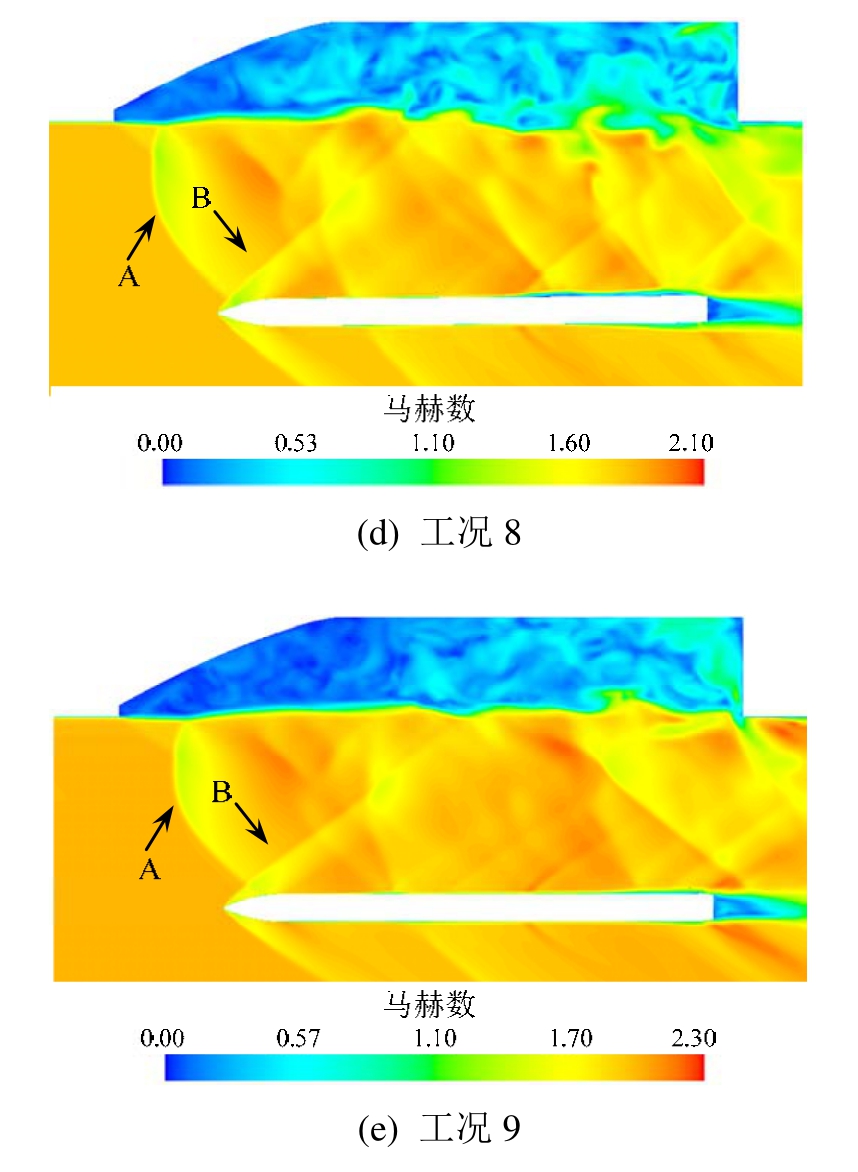
图13 t=0.25 s流场z截面马赫数分布云图
Fig.13 Mach number contour of z cross section for t =0.25 s
由上述分析可知,来流马赫数对弹体下落位移影响较小,亚声速条件下来流马赫数对弹体偏航角度影响也较小。跨声速及超声速时受弹体左右两侧不对称波系结构的影响,弹体均向右侧偏航。在超声速来流条件下,Ma=1.2时弹体偏航及俯仰角度最大,马赫数增大后,流场波系结构对弹体姿态角增长存在一定抑制作用,使得弹体姿态角减小。工况6和工况7机弹分离品质均属于第二类安全分离,其余工况机弹分离品质为第一类安全分离。
3.2 发射速度对弹体下落轨迹影响
在来流马赫数 Ma=1.5条件下,改变弹体初始发射速度,分别取 5 m/s、10 m/s、15 m/s,来探究不同发射速度时弹体下落轨迹变化规律。图 14(a)~图 14(c)为不同发射速度时,弹体竖直方向合力、速度及位移随时间变化曲线。图15(a)~图15(c)为弹体偏航力矩、偏航角速度及偏航角随时间变化曲线。图16(a)~图16(c)为弹体俯仰力矩、俯仰角速度及俯仰角随时间变化曲线。从图 14可以发现,初始发射速度对弹体下落轨迹的影响十分显著。较大的发射速度可以使弹体迅速下落,在短时间内达到安全分离距离,而小的发射速度则会使弹体在载机附近流场滞留更长的时间。当发射速度为15 m/s时,达到 3.5 m下落距离仅用了 0.32 s,而当发射速度为5 m/s时,达到3.5 m下落距离用时增加到0.54 s。
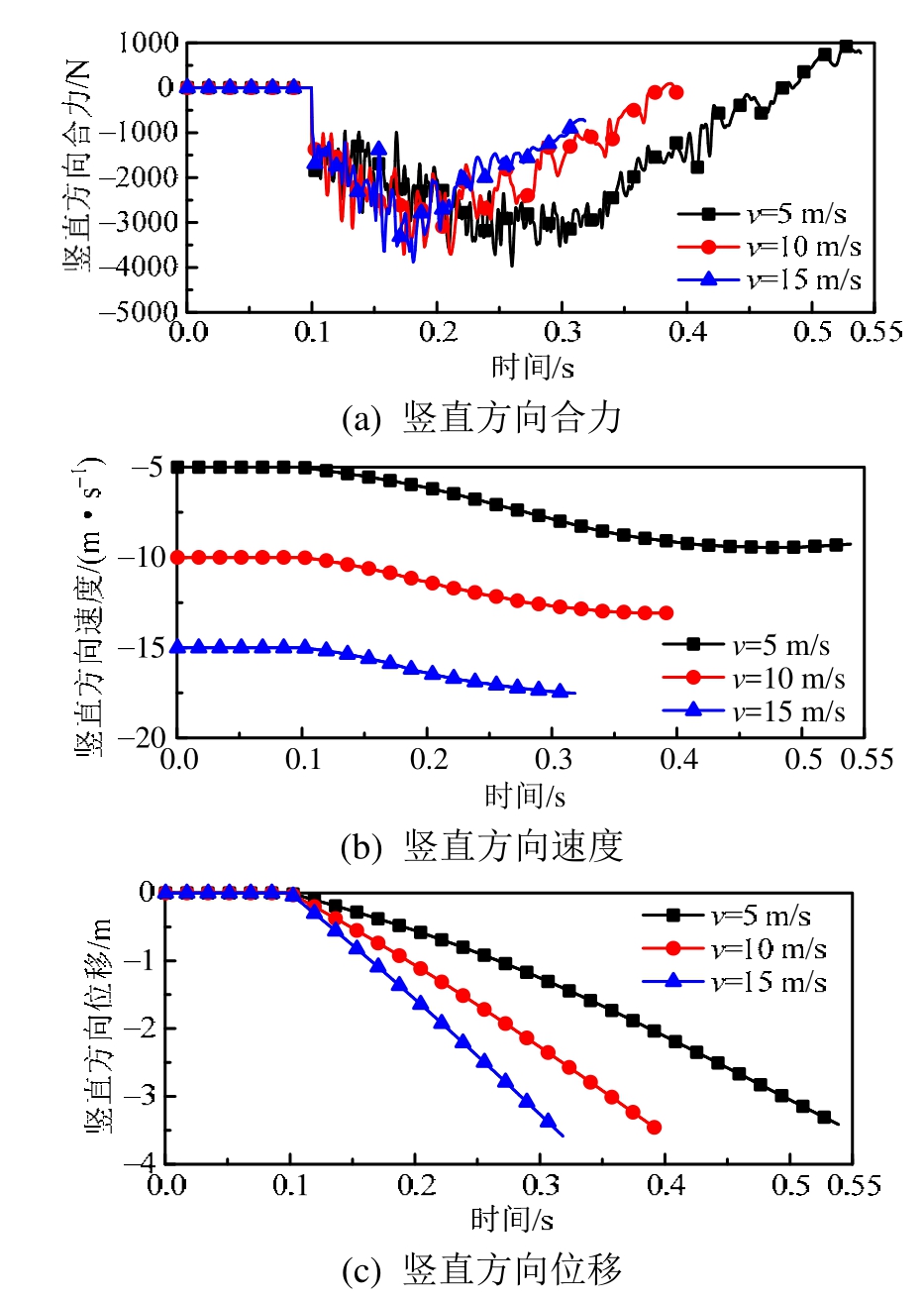
图14 不同初速度竖直方向合力、速度、位移随时间变化
Fig.14 Vertical force, velocity and displacement of missile versus time curves for different launching velocities
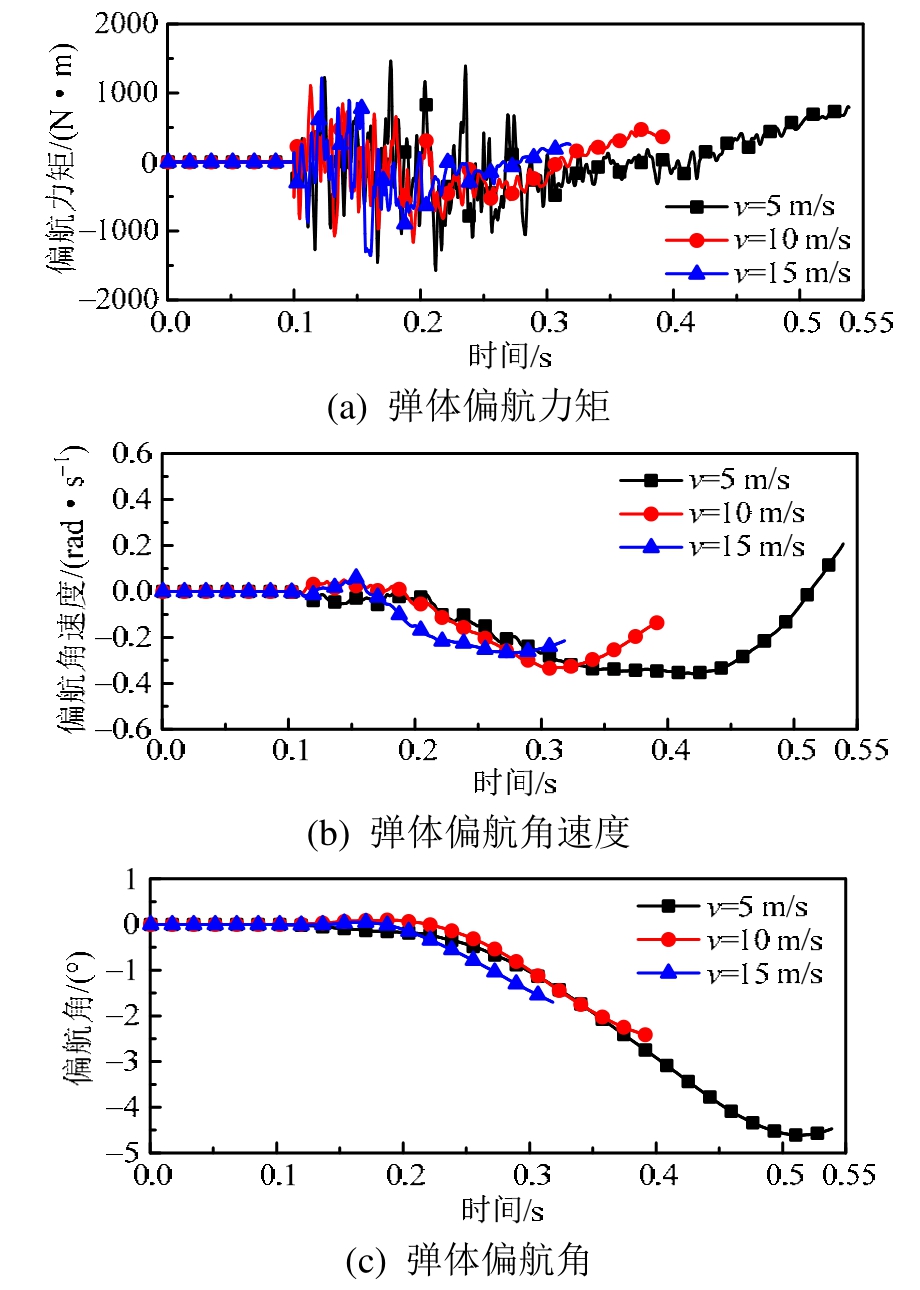
图15 不同初速度偏航力矩、角速度、偏航角随时间变化
Fig.15 Yaw moment, yaw angular velocity and yaw angle of missile versus time curves for different launching velocities
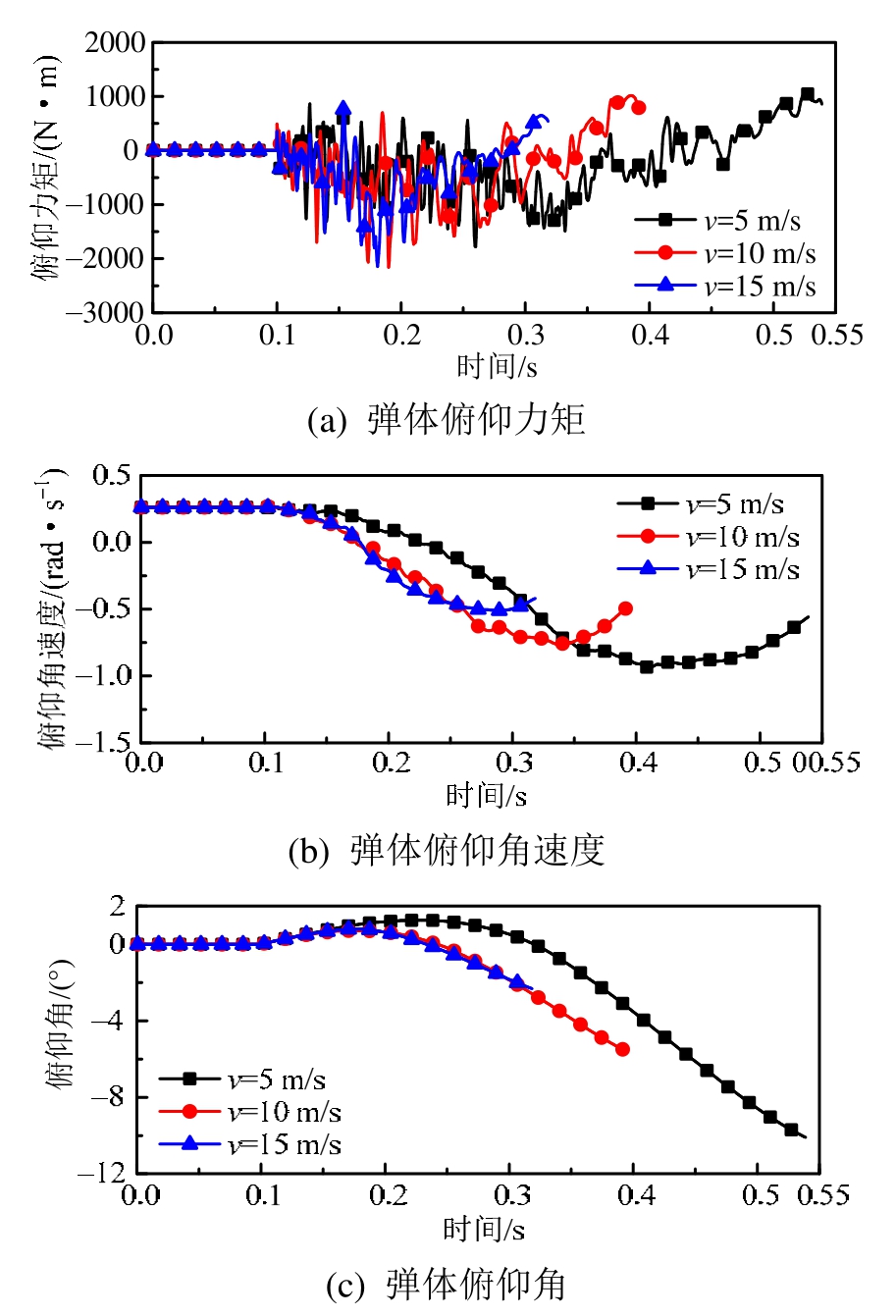
图16 不同初速度俯仰力矩、角速度、俯仰角随时间变化
Fig.16 Pitch moment, pitch angular velocity and pitch angle of missile versus time curves for different velocities
从图 15可以看出,不同工况弹体下落过程中其所受偏航力矩及偏航角速度变化趋势大体保持相同,但是由于弹体下落时间不同,下落结束时弹体最终偏航角并不相同。随着弹体发射速度增加,弹体偏航角度随之减小,当发射速度从5 m/s提升到15 m/s时,弹体右偏航角从4.5°降低为1.5°,如表2所示。从图16可知弹体俯仰角变化趋势与偏航角类似,且变化幅值更大,从10°降为2°。
表2 不同工况弹体下落参数
Tablee 2 Falling parameters for different cases
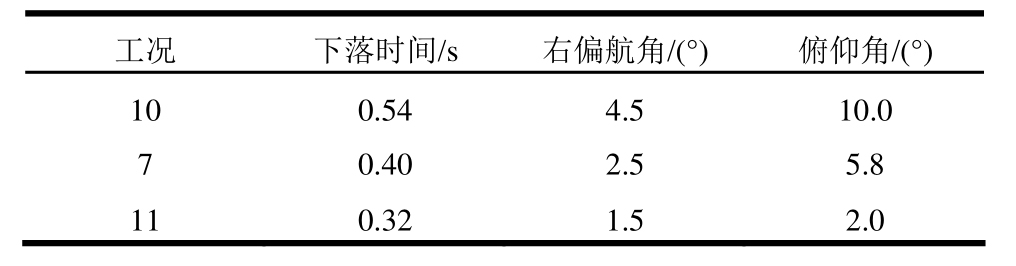
从上述分析可以看出,工况 10中弹体下落速度为5m/s时弹体下落轨迹属于第三类安全分离,当弹体下落速度提高到10 m/s时,弹体分离品质提升为第二类安全分离,当工况 11中下落速度继续增加到15 m/s时,弹体可以快速远离载机且无明显姿态角变化,分离品质最好,为第一类安全分离。针对本文算例,选取v=15 m/s已经可以保证导弹发射具有优良的机弹分离品质。
3.3 发射角速度对弹体下落轨迹影响
从3.2节分析中可以看出,增加弹体发射速度可以显著提升弹体分离品质,但是提升发射速度需要更大的弹射力,这对弹射设备提出更高的要求,增加其设计难度,同时带来设备重量增加等负面问题。在不改变弹体弹射力的情况下,可以改变弹射力作用点的位置来改变弹体弹射力矩大小,即在不改变初始发射速度的情况下,可以改变弹体发射角速度φ来改变弹体分离品质。为了探究不同φ值对弹体下落轨迹的影响规律,分别取 φ=0 °/s、15 °/s、30 °/s,以弧度制表示为 φ=0.0 rad/s、0.2618 rad/s、0.5236 rad/s,来流马赫数仍保持为Ma=1.5。
图17(a)~图17(c)为不同发射角速度,弹体竖直方向合力、速度及位移随时间变化曲线。图18(a)~图18(c)为弹体俯仰力矩、俯仰角速度及俯仰角随时间变化曲线。由于φ值改变对弹体偏航姿态角影响较小,故不再详细给出。图 19为不同工况对应的弹体下落轨迹。图中虚线表示弹体姿态角由低头姿态转为抬头姿态的位置。从图 18可知不同工况下弹体俯仰姿态角变化趋势存在明显的差异。工况12中不给弹体施加初始低头角速度,受舱体唇口剪切层及流场波系影响弹体下落后迅速抬头,在计算结束时弹体俯仰角度达到8°。当给弹体施加初始低头角速度之后,弹体下落初期先低头,使弹体以低头姿态出舱,减小了剪切层对弹体下落的不利影响。弹体俯仰角度随着初始低头角速度的增加而减小,φ=0.2618 rad/s时弹体最终俯仰角度由 8°减小为5.8°,当φ=0.5236 rad/s时弹体俯仰角度进一步减小为 2.5°。
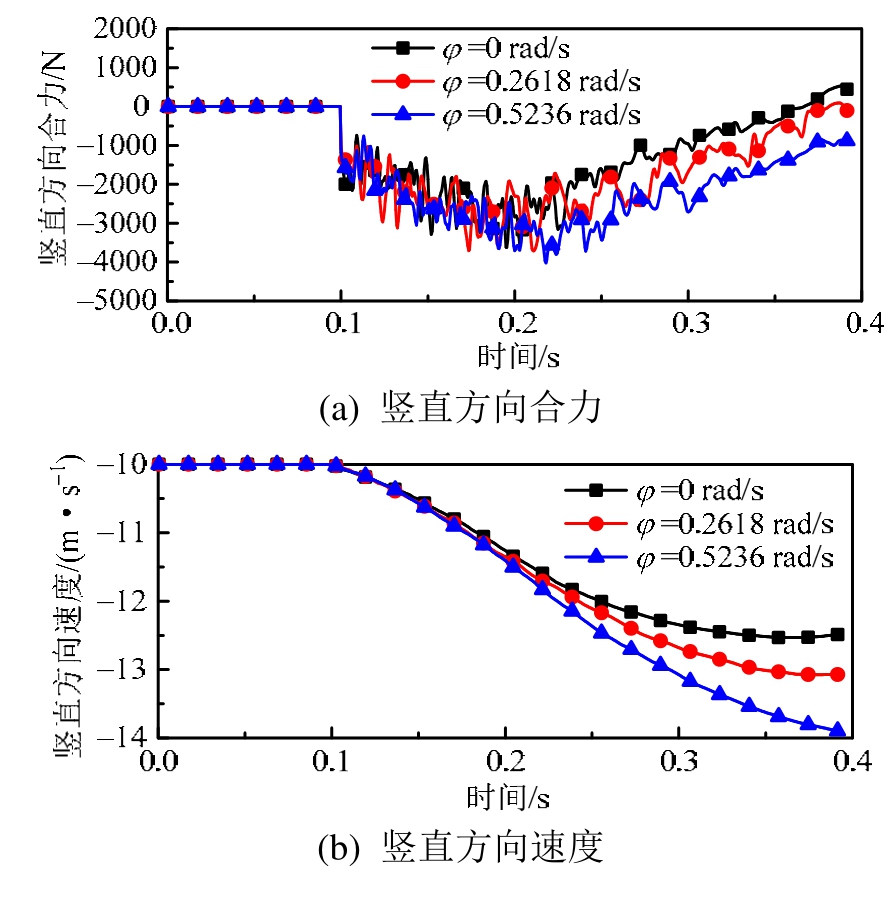
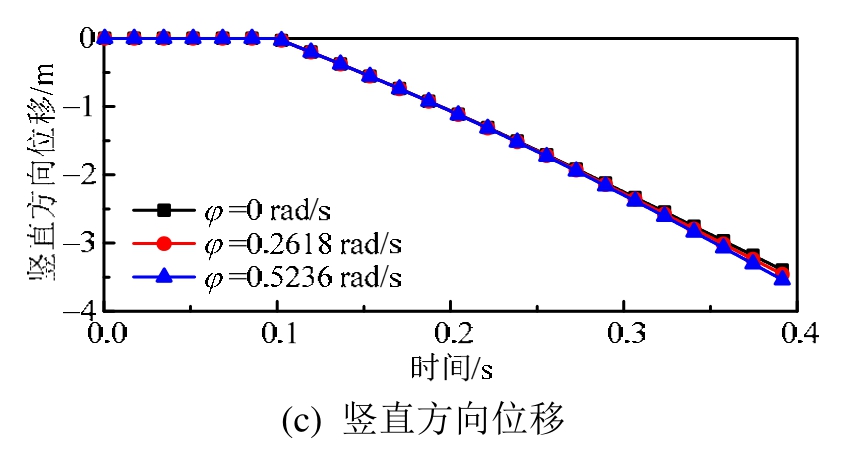
图17 不同角速度竖直方向合力、速度、位移随时间变化
Fig.17 Vertical force, velocity and displacement of missile versus time curves for different angular velocities
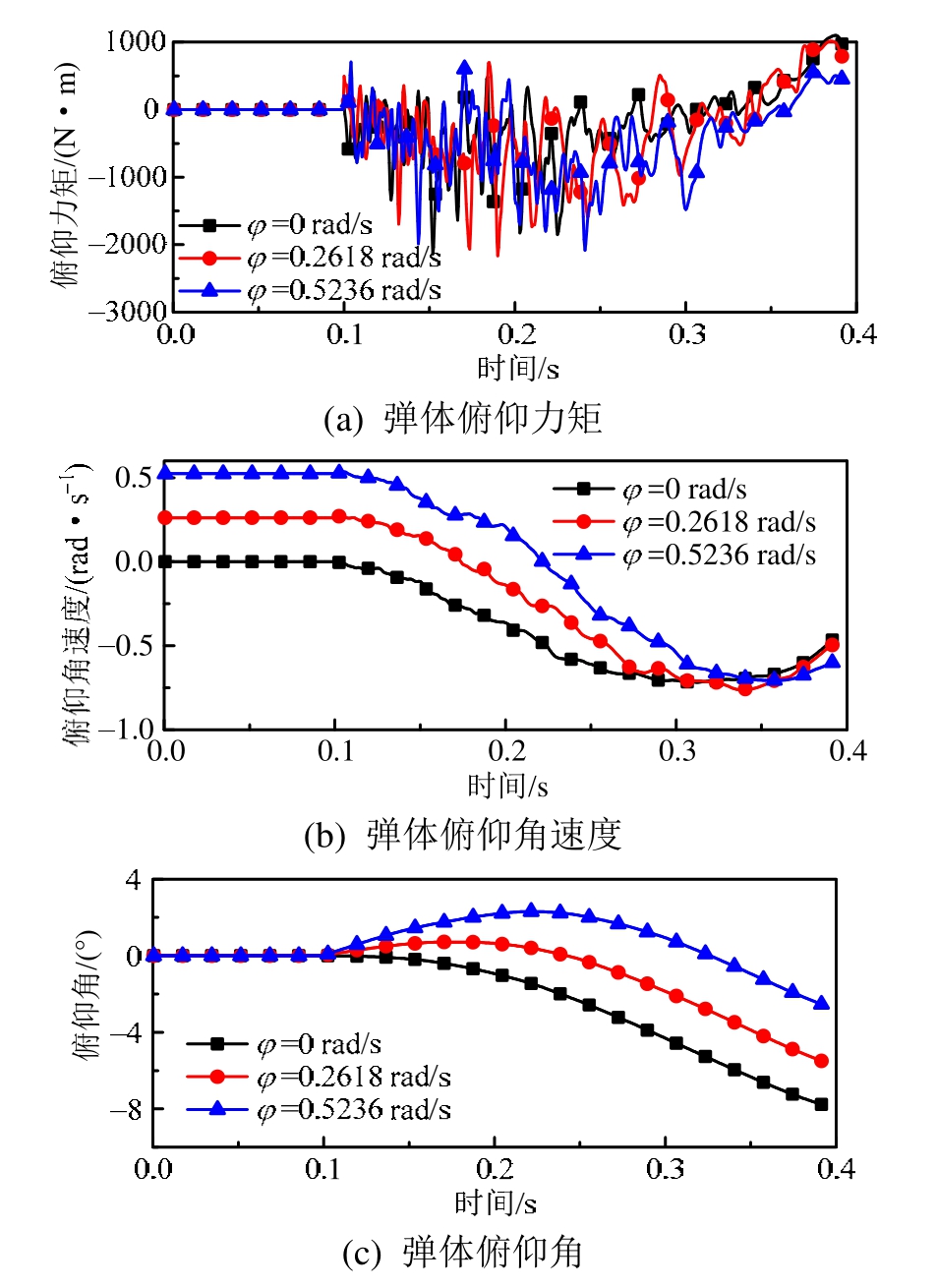
图18 不同角速度俯仰力矩、角速度、俯仰角随时间变化
Fig.18 Pitch moment, pitch angular velocity and pitch angle of missile versus time curves for different angular velocities
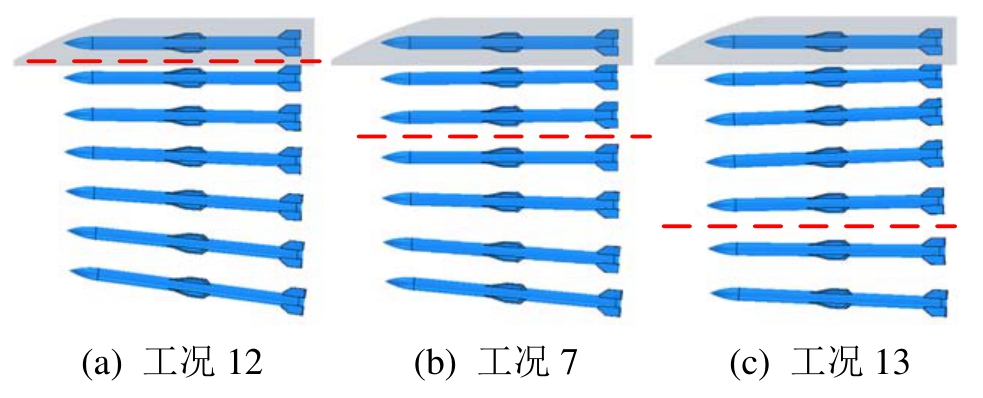
图19 不同发射角速度弹体下落轨迹
Fig.19 Store trajectory for different angular velocities
从图19可以看出,随着φ的增大,下落初期低头角度增大,弹体姿态角由低头姿态转为抬头的时间被推迟。弹体在流场中为低头姿态时,其上表面为气流迎风面,来流撞击在上表面,一部分动能转化为压能,使上表面压力高于下表面,弹体竖直方向受到的气动力向下,与重力方向相同,竖直方向合力为二者之和。弹体低头角度越大,上下表面压力差越大,弹体受到的向下的气动力合力越大,同时弹体保持低头时间越长,越有利于弹体下落速度的增长。从图17可以看出,随着φ的增加,弹体下落速度随之增大,工况13中t =0.4 s时弹体下落速度增长到14 m/s,而工况12中弹体下落速度增幅较小为12.5 m/s。
从上述分析可以看出,增加弹体的初始低头角速度不仅有利于减小弹体姿态的变化,还可以提高弹体分离速度,有利于机弹安全分离。工况 12弹体分离品质属于第二类安全分离,工况 13中将发射角速度提升到φ =0.5236 rad/s时,弹体分离品质提高为第一类安全分离。在不增加弹体弹射力的情况下通过改变弹射力的作用位置,来改变弹体初始发射角速度同样可以有效的提升机弹分离品质。
4 结论
(1) 对于不同来流马赫数,弹体下落位移变化较小。亚声速条件下来流马赫数对弹体偏航角度影响也很小。跨声速及超声速时受弹体左右两侧不对称波系结构的影响,弹体均向右侧偏航。超声速来流条件下,Ma=1.2时弹体偏航及俯仰角度最大,机弹分离品质最差。随着马赫数增加,流场波系结构对弹体姿态角增长存在一定抑制作用,弹体姿态角变化幅度随之降低,机弹分离品质得到提升。
(2) 增加弹体发射速度可以使弹体更快的达到安全分离距离,缩短弹体在载机流场中的滞留时间,同时还可以减小弹体姿态角的变化,当发射速度从5 m/s增加到15 m/s时,弹体下落时间由0.54 s缩短为0.32 s,弹体偏航角由4.5°降低为1.5°,俯仰角由 10°降低为 2°。
(3) 在不改变弹射力大小的前提下,可以通过改变弹射力作用位置来改变弹体发射角速度的大小。增加弹体的初始低头角速度不仅可以减小弹体俯仰角度,推迟弹体抬头时间,还可以提高弹体分离速度,有利于机弹安全分离。
参考文献:
[1]杨党国, 李建强, 蒋卫民, 等. 不同马赫数下长深比对空腔声学特性的影响[J]. 工程力学, 2011, 28(12):221―225.Yang Dangguo, Li Jianqiang, Jiang Weimin, et al.Investigation on aero-acoustic characteristics inside cavities influenced by length-depth ratios at different Mach numbers [J]. Engineering Mechanics, 2011,28(12): 221―225. (in Chinese)
[2]Johnson R A, Stanek M J, Grove J E. Store separation trajectory deviations due to unsteady weapons bay aerodynamics [C]// 46th AIAA Aerospace Sciences Meeting and Exhibit, Reno Nevada, AIAA, 2008: 1―15.
[3]Davis M B, Pat Y, Smith B R. Store trajectory response to unsteady weapons bay flow fields [C]// 47th AIAA Aerospace Sciences Meeting, Orlando Florida, AIAA,2009: 1―35.
[4]Kim D H, Choi J H, Kwon O J. Detached eddy simulation of weapons bay flows and store separation [J].Computers & Fluids, 2015, 121(7): 1―10.
[5]Westmoreland W S. Trajectory variation due to an unsteady flow Field [C]// 47th AIAA Aerospace Sciences Meeting, Orlando Florida, AIAA, 2009: 125―138.
[6]Babu S V, Loupy G, Dehaeze F. Aeroelastic simulations of stores in weapon bays using Detached Eddy Simulation [J]. Journal of Fluids and Structures, 2016,66(7): 207―228.
[7]唐上钦, 黄长强, 翁兴伟. 考虑气动干扰的导弹内埋式发射弹道研究[J]. 弹箭与制导学报, 2013, 33(3):138―142.Tang Shangqin, Huang Changqiang, Weng Xingwei. The study on trajectory of missile separating from cavity with aerodynamic interference considered [J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2013, 33(3):138―142. (in Chinese)
[8]郭亮, 王纯, 叶斌, 等. 采用流动控制的超声速内埋物投放特性研究[J]. 航空学报, 2015, 36(6): 1752―1761.Guo Liang, Wang Chun, Ye Bin, et al. Investigation on characteristics of store release from internal bay in supersonic flow under flow control [J]. Acta Aeronauiica et Astronautica Sinica, 2015, 36(6): 1752―1761. (in Chinese)
[9]吴继飞, 罗新福, 徐来武, 等. 内埋武器分离特性及其改进方法研究[J]. 空气动力学学报, 2014, 32(6): 814―819.Wu Jifei, Luo Xinfu, Xu Laiwu, et al. Investigation on internal weapon separation characteristics and flow control methods [J]. Acta Aerodynamica Sinica, 2014,32(6): 814―819. (in Chinese)
[10]张群峰, 闫盼盼, 黎军. 战斗机武器外挂投放与内埋投放比较[J]. 北京航空航天大学学报, 2017, 43(6):1085―1097.Zhang Qunfeng, Yan Panpan, Li Jun. Comparation between external store separation and buried store separation [J]. Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(6): 1085―1097.(in Chinese)
[11]闫盼盼, 张群峰, 金明. 舱门对内埋武器分离特性影响分析[J]. 兵工学报, 2017, 38(6): 1120―1130.Yan Panpan, Zhang Qunfeng, Jin Ming. Effect of bay door on separation characteristics of internal sotre [J].Acta Armamentarii, 2017, 38(6): 1120―1130. (in Chinese)
[12]Blazek J. Computational fluid dynamics principles and applications [M]. London: Elsevier, 2005: 16―18.
[13]刘伟. 细长机翼摇滚机理的非线性动力学分析及数值模拟方法研究[D]. 长沙: 国防科技大学, 2004: 25―34.Liu Wei. Nonlinear dynamics analysis for mechanism of slender wing rock and study of numerical simulation method [D]. Changsha: National University of Defense Technology, 2004: 25―34. (in Chinese)
[14]Venkatakrishnan V. On the accuracy of limiters and convergence to steady state solutions [C]// 31st Aerospace Sciences Meeting, Reno Nevada: AIAA,1994: 152―164.
[15]Shur M L, Spalart P R, Strelets M. A hybrid RANS-LES approach with delayed-DES and wall-modelled LES capabilities [J]. International Journal of Heat and Fluid Flow, 2008, 29(6): 1638―1649.
[16]董祥瑞, 陈耀慧, 董刚, 等. 高超声速激波/边界层干扰及 MVG阵列流动控制研究[J]. 工程力学, 2016,33(7): 23―30.Dong Xiangrui, Chen Yaohui, Dong Gang, et al. Studies on hypersonic shock wave/boundary layer interactions and flow control based on MVG array [J]. Engineering Mechanics, 2016, 33(7): 23―30. (in Chinese)
[17]Menter F R. Two-equation eddy-viscosity turbulence modeling for engineering applications [J]. AIAA Journal,1994, 32(8): 1598―1605.
[18]Spalart P R, Jou W H, Strelets M, et al. Comments on the feasibility of LES for wings, and on a hybrid RANS/LES approach [C]// 1st AFOSR International Conference on DNS/LES, Columbus, Greyden Press, 1997: 4―8.
[19]Spalart P R, Deck S, Shur M L, et al. A new version of detached eddy simulation, resistant to ambiguous grid densities [J]. Theoretical and Computational Fluid Dynamics, 2006, 20(3): 181―195.
[20]Durbin P. Statistical theory and modeling for turbulent flows [M]. New York: Wiley, 2011: 302―308.
[21]阎超. 计算流体力学方法及应用[M]. 北京: 北京航空航天大学出版社, 2006: 197―217.Yan Chao. The computational fluid dynamics method and its application [M]. Beijing: Beijing University of Aeronautics and Astronautics Press, 2006: 197―217. (in Chinese)
[22]张来平, 邓小刚, 张涵信. 动网格生成技术及非定常计算方法进展综述[J]. 力学进展, 2010, 40(4): 424―447.Zhang Laiping, Deng Xiaogang, Zhang Hanxin. Reviews of moving grid generation techniques and numerical methods for unsteady flow [J]. Advances in Mechanics,2010, 40(4): 424―447. (in Chinese)
[23]Heim E R. CFD wing/pylon/fin store mutual interference wind tunnel experiment [R]. Tennessee: Arnold Engineer Development Center, 1991: 25―34.
[24]郑书娥, 廖志忠. 空空导弹机弹分离安全性研究[J].四川兵工学报, 2015, 36(5): 17―23.Zheng Shu’e, Liao Zhizhong. Study on air-to-air missile safety separation technology from craft [J]. Journal of Sichuan Ordnance, 2015, 36(5): 17―23. (in Chinese)