预应力自复位混凝土结构,主要优点是将结构的非线性变形集中于连接区域,其它部分基本保持弹性,而且由于预应力筋的回弹作用,结构残余变形很小,可实现震后结构功能的迅速恢复,代表可持续发展工程抗震的研究方向。近年来得到较多学者的关注,成为预制结构研究的热点之一。
耗能部件是预应力预制结构体系研究的热点。国内外学者提出了大量的耗能部件构造形式,取得较多的研究成果[1―5],但也存在如下问题:1) 国内外学者均较多地关注预应力拼接钢结构的耗能部件,对预应力预制混凝土结构的耗能部件研究较少,仅提出少数的几种形式,如常见的在梁端开槽埋置耗能钢筋,该构造的施工及后期的更换较不方便,腹板摩擦式预应力预制框架结构需在节点及梁端预埋较大块的钢板且对构件的平整度要求较高。为了促进预应力预制混凝土结构的发展和工程应用,进一步开发构造简单、施工方便、受力明确的耗能部件是关键。作者以角钢作为耗能元件,提出新型的基于角钢-高强螺栓连接的预应力自复位混凝土框架结构(下文简称 PTED结构),并进行了系列的试验研究[6]。为了构建节点的恢复力模型,在试验研究的基础上,建立骨架曲线的理论表达并基于试验数据建立能反映其滞回规则的控制方程,为结构有限元分析模型的建立和设计理论的构建提供支撑。
1 试验概况
针对PTED节点的梁高hb、预应力筋的有效应力fpi及角钢厚度ta、长度la等参数,进行系统的边节点试验研究[6],试验参数见表1,试验模型见图1。
表1 试验参数
Table 1 Test parameters
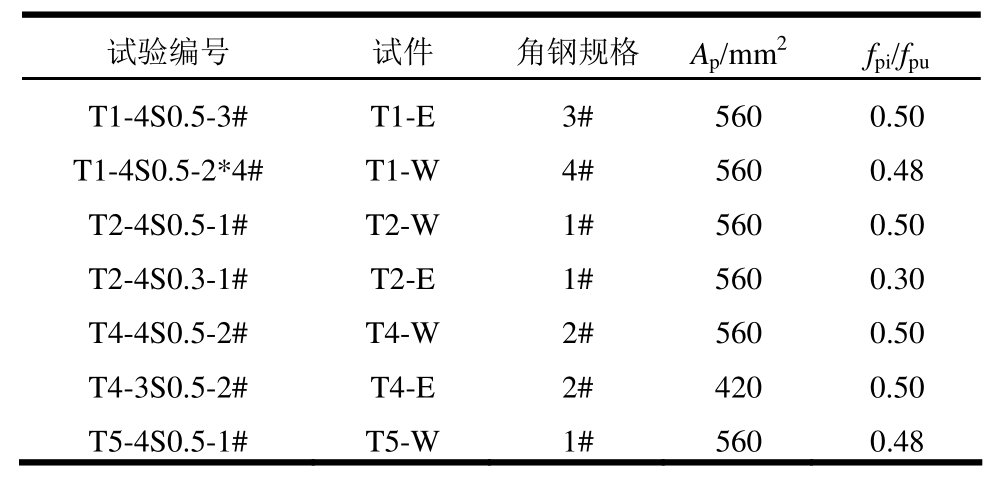
注:1) 以 T2-4S0.5-1#为例,说明试件的命名方式:T2为节点编号,4为预应力筋根数,0.5为预应力筋有效应力fpi与极限强度fpu的比值;1#为耗能角钢规格。2) T2-W、T2-E分别表示利用T2节点的西侧梁、东侧梁进行边节点试验。

图1 试验模型
Fig.1 The model of the tests
2 滞回恢复力模型
2.1 骨架曲线
PTED节点F-Δ曲线(F为梁端荷载,Δ为梁端位移)有几个关键点,分别表征以下几个极限状态[7]:1) 有效线性极限状态(对应的荷载、位移记为Fe、Δe);2) 角钢屈服极限状态(对应的荷载、位移记为Fy、Δy);3) 梁端约束混凝土被压碎极限状态(对应的荷载、位移记为Fc、Δc)。为了保证预应力筋在大震下仍处于弹性阶段,预应力筋沿梁长通长无粘结,预应力筋屈服较迟,故不考虑预应力筋屈服极限状态。骨架曲线简化为三折线模型,见图2。
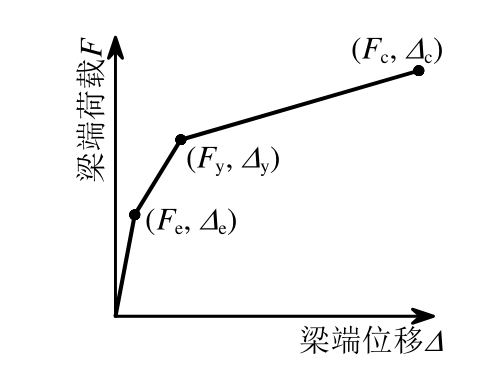
图2 骨架曲线的三折线模型
Fig.2 Trilinear skeleton curve model
2.1.1 有效线性极限状态
有效线性极限状态是指梁端荷载与位移曲线开始偏离线性变化的临界状态,即软化点。梁的软化可由下列两种情况引起:1) 梁端缝隙的张开(对应的弯矩Me1,见图 3(a));2) 受压区混凝土的应力-应变曲线出现明显的非线性变化(对应的弯矩Me2,见图3(b))。此时近似认为预应力筋的应力为初始应力。忽略角钢的受力对此状态的影响。
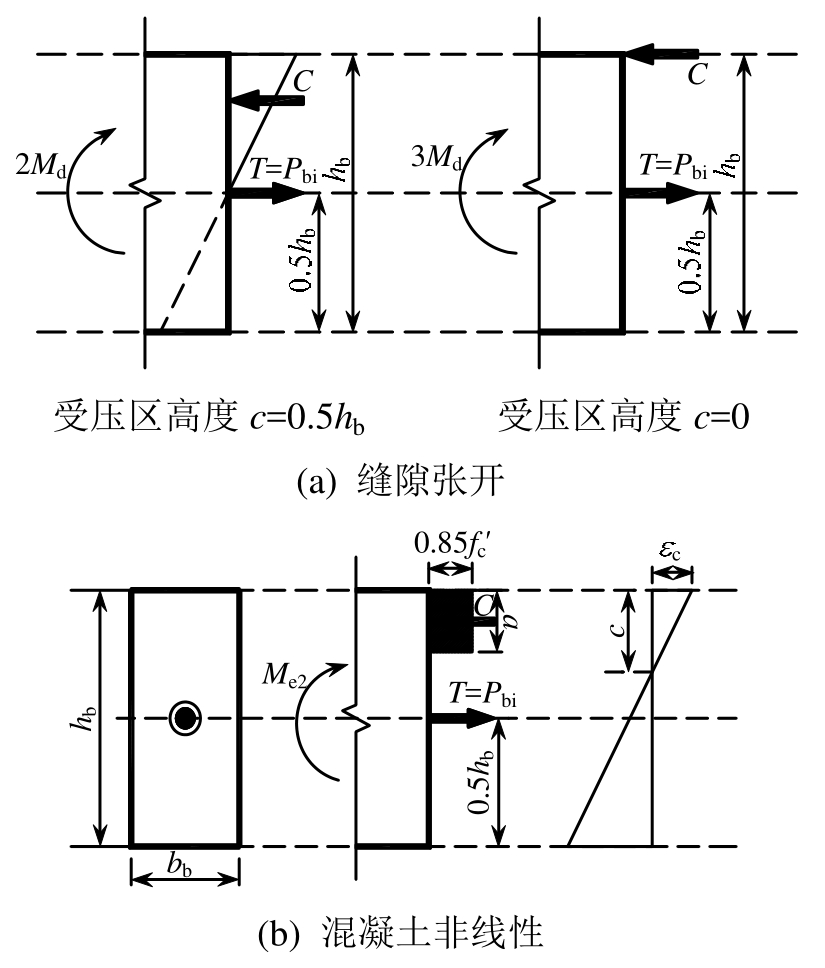
图3 有效线性极限状态梁端受力示意图
Fig.3 Force diagrams at the beam end
根据 El-Sheikh的分析结果可知,梁端缝隙张开引起的有效线性极限状态对应的受压区高度c介于0~0.5hb。El-Sheikh最终推荐 Me1= 2.5Md(Md为消压极限状态(最外层混凝土纤维的预压应力为 0)对应的梁端弯矩值),即采用 c= 0.25hb确定缝隙的张开引起的梁端弯矩[8],本文亦采用这一假定。
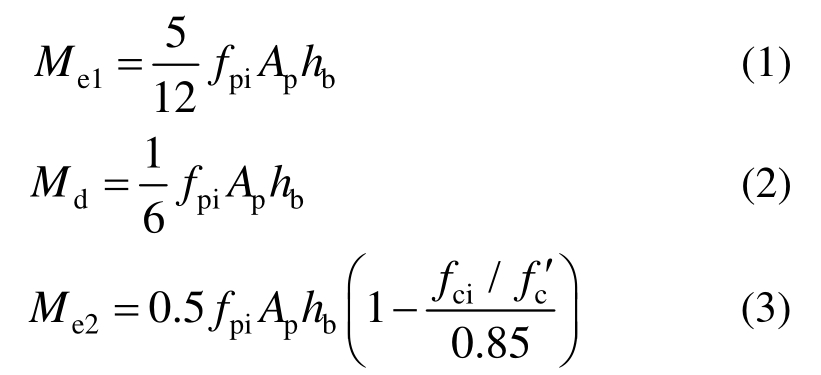
则梁端弯矩Me为:
梁端转角eθ为:
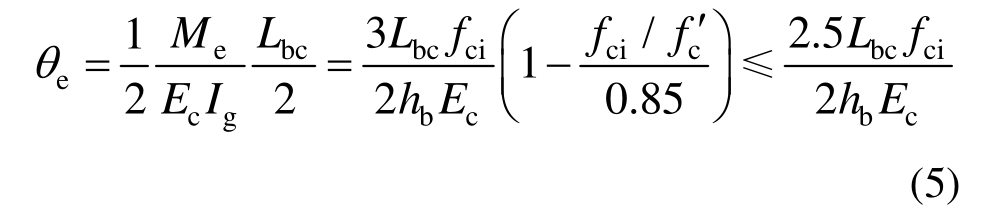
式中:fpi为预应力筋初始应力;Ap为预应力筋面积;hb为梁高;fci为梁截面平均初始压应力;Lbc为加载点到梁柱结合面的距离,fc′为无约束混凝土的轴心抗压强度。
梁端荷载Fe=Me/Lbc,梁端位移Δe=θeLbc。
2.1.2 角钢屈服极限状态
角钢屈服极限状态是指耗能角钢开始屈服的极限状态,角钢屈服极限状态节点变形如图4所示。
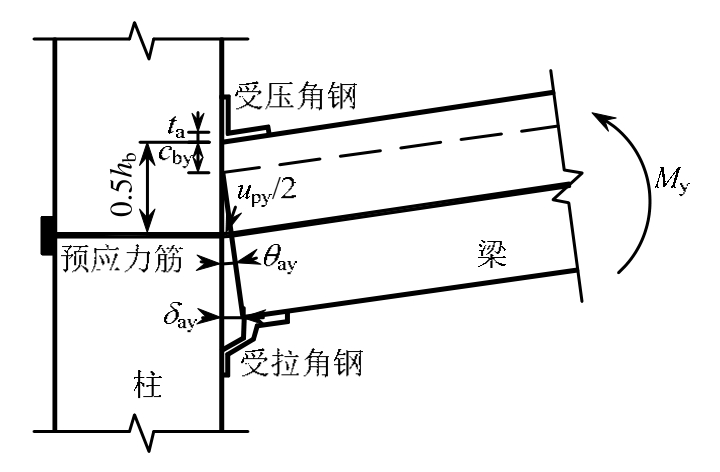
图4 节点变形示意图
Fig.4 Deformation of the joints
计算角钢屈服极限状态对应的梁端荷载 Fy与Δy变形基于以下假定[7]:
① 受拉角钢水平肢的轴力等于受拉角钢的屈服荷载Tay
[9];
② 受压角钢水平肢内力为[10]:
式中:fay为角钢材料的屈服强度;Aa为角钢肢截面面积;Cas为角钢与梁的接触面发生相对滑移时板件间的摩擦力;
③ 梁柱结合面处梁端压应力均匀分布,应力值为无约束混凝土轴心抗压强度 fc′,见图5(a);
④ 忽略保护层混凝土压碎对该状态的影响。
计算步骤如下:
1) 假设此状态下预应力筋合力等于初始预应力筋合力,即:
式中,Pbi为预应力筋的初始合力,Pbi=Apfpi。
2) 由假定①、②可得梁端受压区混凝土合力:
3) 由假定③得梁端受压区混凝土高度为:
4) 计算梁端相对转角:
式中:δay为角钢受拉屈服的变形值;ta为角钢厚度。
5) 计算预应力筋的伸长值:
6) 计算预应力筋合力:
式中:Lpu为预应力筋的无粘结长度;Ep为预应力筋的弹性模量。
7) 若式(12)算得的Py与式(7)的Py不吻合,则将式(12)算得的Py代入式(7),2)步~6)步重新计算,直到式(12)和式(7)的Py值收敛。
8) 对梁截面形心取矩,计算梁端弯矩为:
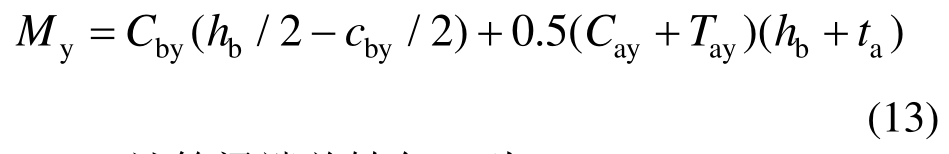
9) 计算梁端总转角yθ为:
式中,Kbi为节点的弹性转角刚度。
10) 梁端荷载为:
梁端位移为:
2.1.3 约束混凝土被压碎极限状态
约束混凝土被压碎极限状态定义为核心区混凝土最外层纤维应变达到极限压应变εcu。
约束混凝土被压碎极限状态对应的梁端荷载Fc与位移Δc采用迭代法计算,基于如下假定[7]:
① 受拉角钢水平肢轴力 Tac=2Tay;
② 受压角钢水平肢轴力为Cac=Tac≤Cas;
③ 梁端受压区混凝土应力呈矩形分布,应力大小为约束混凝土极限抗压强度![]() 见图5(b);
见图5(b);
④ 由于仅梁端角部有轻微的压碎迹象,梁端塑性铰长度较小,取Lcr=max{cbc,bc/4},见图6。式中 cbc为约束混凝土被压碎极限状态时的梁端受压区高度;bc为梁端混凝土核心区宽度;
⑤ 忽略保护层混凝土的作用。
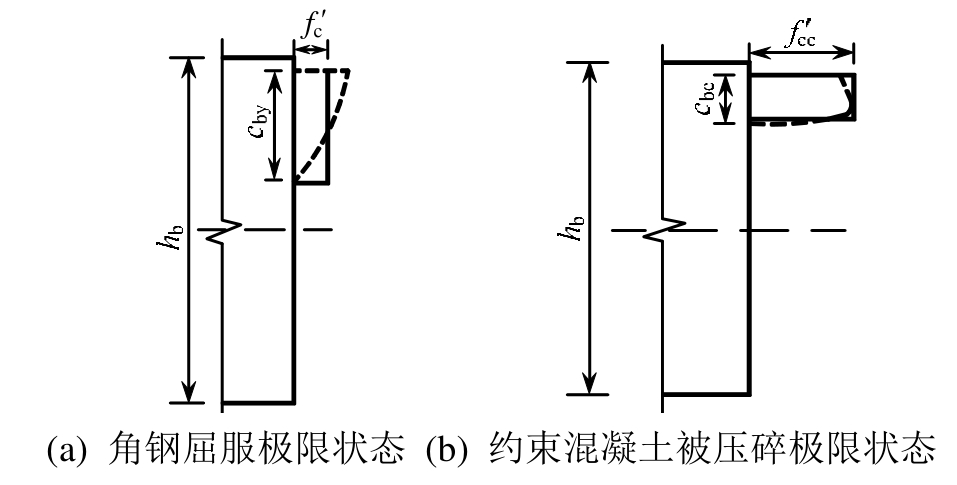
图5 梁端混凝土应力状态
Fig.5 Concrete stress state at the beam end
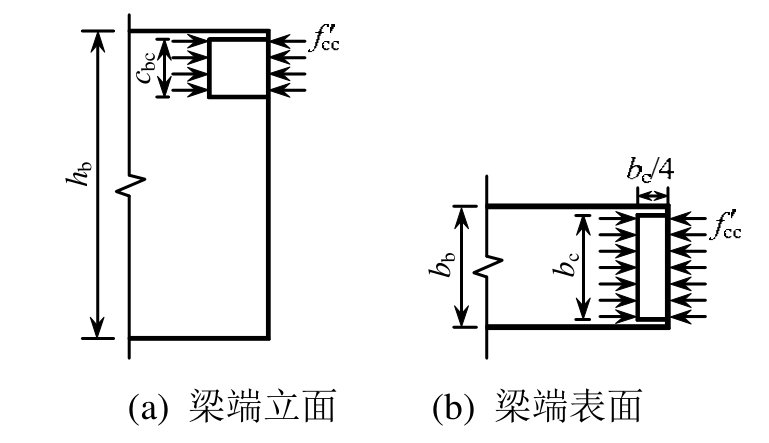
图6 梁端塑性铰长度取值
Fig.6 The plastic hinge length at the beam end
计算步骤如下:
1) 假设预应力筋合力:
2) 由假定①和②,计算梁端混凝土压力:式中Tac=2Tay。
3) 由假定③计算梁端受压混凝土高度:
4) 对梁截面形心取矩,计算梁端弯矩Mc:
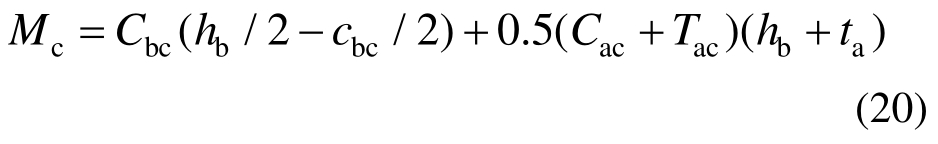
5) 计算梁端塑性曲率:
6) 计算梁端塑性转角:
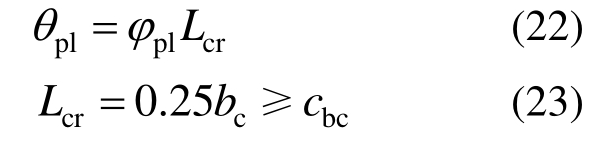
7) 计算梁端弹性转角:
式中,Kbi为节点的弹性转角刚度。
8) 计算梁端总的转角为:
9) 计算预应力筋的伸长值:
10) 计算预应力筋合力:
式中,Py为预应力筋的屈服合力,Py=Apfpy
11) 若式(27)算得的 Pc与式(17)的 Pc不吻合,则将式(27)算得的 Pc代入式(17),2)步~10)步重新计算,直到式(27)和式(17)的 Pc收敛为止。
12) 计算梁端荷载:
计算梁端位移:
基于条带法,利用FORTRAN语言编制PTED节点角钢屈服极限状态和约束混凝土被压碎极限状态的计算程序,计算流程图见图7、图8。

图7 角钢屈服极限状态计算流程图
Fig.7 calculation flow chart for the angle steel yield limit state

图8 约束混凝土被压碎极限状态计算流程图
Fig.8 calculation flow chart for the concrete crush limit state
2.2 滞回规则
PTED节点(图9对应的T3-4s0.5-1#)的梁端荷载FPTED可由对应的PT节点(仅有预应力筋连接,图9对应的T3-4s0.5)的梁端荷载FPT和ED节点(仅有角钢连接,图9对应的T3-1#)的梁端荷载FED叠加得到[11]。
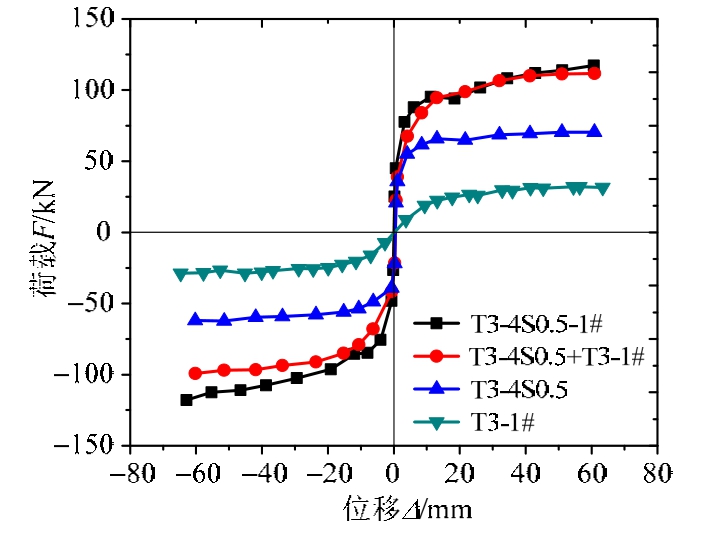
图9 各试件的骨架曲线[11]
Fig.9 Skeleton curves of test specimens
由试验结果可知[11],PT节点(仅有预应力筋连接)的滞回模型如图10(a)所示,呈非线性弹性;ED节点(仅有角钢连接)的滞回模型呈刚度退化模型(图10(b))。在预应力筋和角钢的共同作用下,PTED节点的滞回模型呈旗形模型(图10(c)),即节点具有自复位能力的同时,兼备一定的耗能能力。

图10 PTED节点F-Δ滞回模型
Fig.10 F-Δ restoring force model
图10(a)中β为考虑混凝土轻微损伤产生的滞回耗能参数,根据试验结果建议β取值为:λ =1.0,β =0.15;λ =0.5,β =0.35;中间按线性插值取值(λ为预应力度,定义为极限状态下由预应力筋提供的抵抗弯矩与截面总抵抗弯矩的比值)。图 10(a)中 A点为有效线性极限状态点,C点为卸载点,D点在卸载路径上,E点为卸载到与加载路径重合点。图 10(b)中B点为角钢屈服点。图10(c)在O→A时,PTED节点保持弹性,梁柱连接处缝隙未张开;在A→B时,梁柱连接处缝隙张开,PTED节点进入非线性弹性状态,节点刚度减小;在B→C时,由于角钢屈服,PTED节点的刚度进一步衰减。
图10(c)可由图10(a)和图10(b)叠加而成,则:

式中:FA、FB分别对应PTED节点的有效线性极限状态和角钢屈服极限状态对应的荷载;k1为预应力筋提供的节点弹性刚度;k2为预应力筋提供的节点非线性弹性刚度;k3为角钢提供的节点弹性刚度;k4为角钢提供的节点屈服后刚度。
由图10(c)可知,在梁柱连接处缝隙张开(A点)之前,梁端已有位移产生,主要由梁的弯曲和剪切变形引起。
需要指出,为保证节点具有较好的自复位能力,需满足F(PTED)E>0,即|F(PT)E|>|F(ED)E|,F(PT)E、F(ED)E、F(PTED)E分别为图10(a)、图10(b)、图10(c)中E点对应的荷载值。
3 计算值与试验结果的对比
3.1 骨架曲线的对比
图 11给出理论计算所得骨架曲线与试验结果的比较,图中F为梁端荷载,Δ为梁端位移。由图 11可知,理论计算结果与试验结果吻合较好,采用三折线模型可较好地预测PTED节点的F-Δ的关系。表2给出各极限状态对应的承载力和变形。表中Fe、Fy、Fm及Δe、Δy、Δm分别是有效线性极限状态、角钢屈服极限状态以及约束混凝土被压碎极限状态对应的梁端荷载及变形。
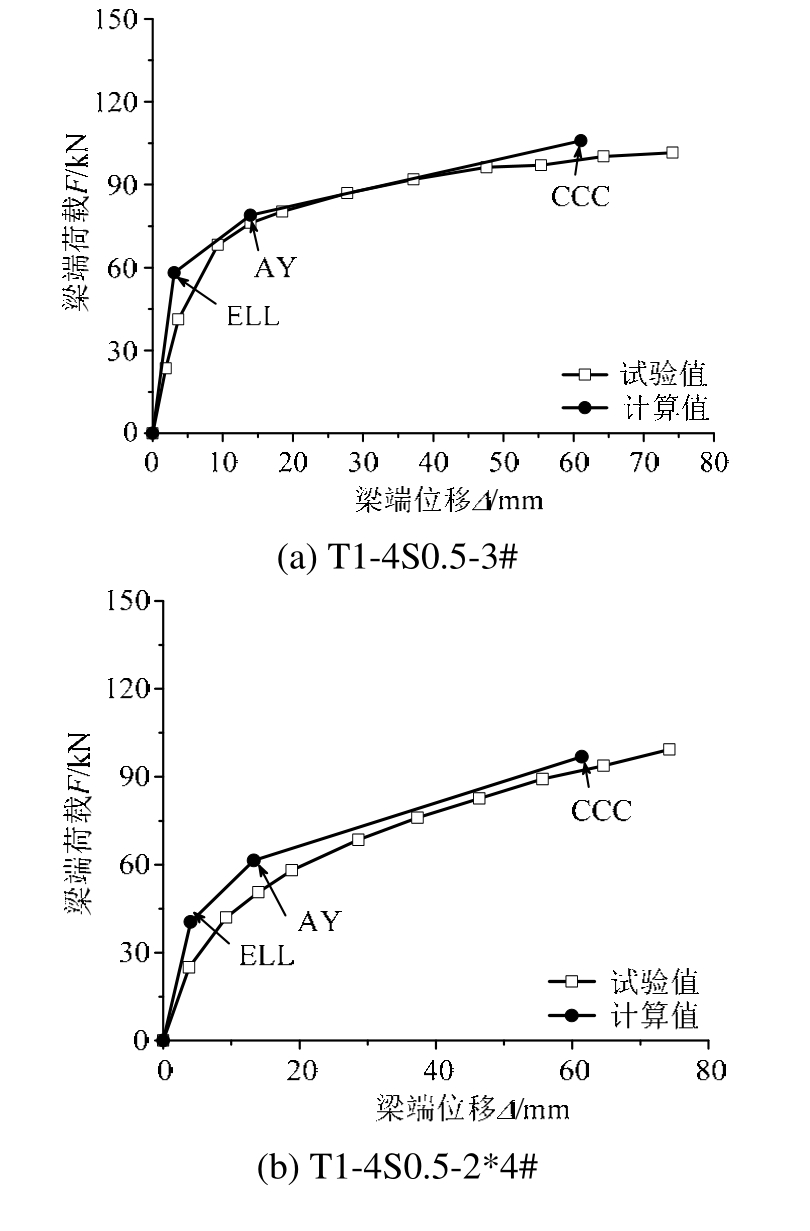

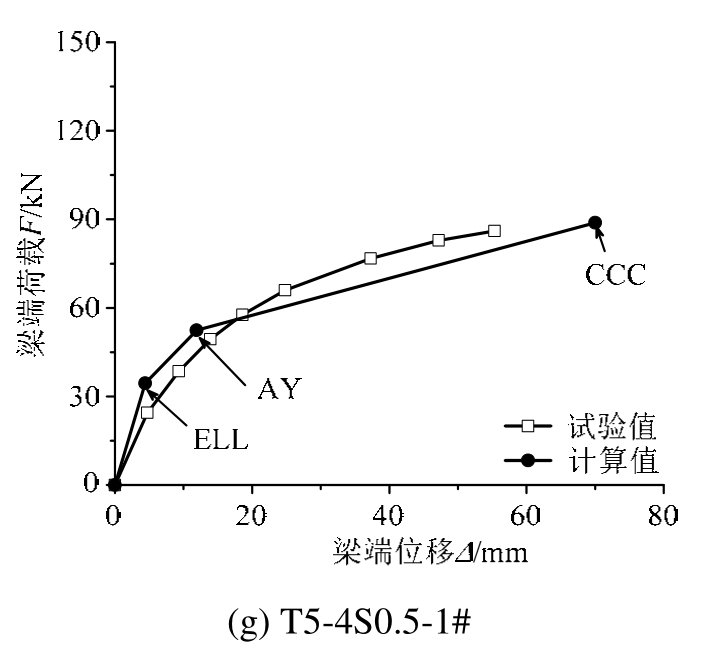
图11 骨架曲线计算值与试验值的比较
Fig.11 The comparisons of calculated and experimental skeleton curves
注:ELL-有效线性极限状态;AY-角钢屈服极限状态;CCC-约束混凝土被压碎极限状态
表2 骨架曲线计算值与试验值的对比
Table 2 The comparisons of calculated and experimental skeleton curves
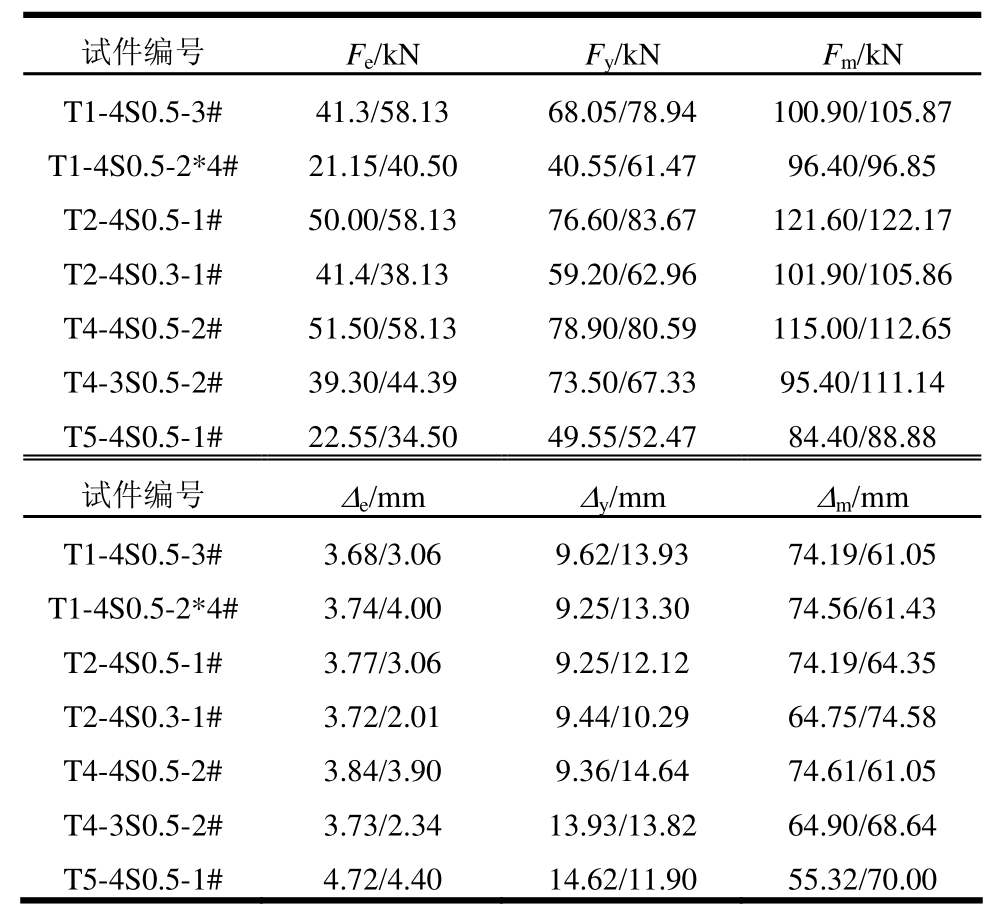
注:表格内前一个数字为试验结果,后一数字为理论计算结果。
3.2 预应力筋合力的计算值与试验值对比
在侧向荷载作用下,梁柱接触面上缝隙张开使预应力筋伸长,应力增大。由预应力筋合力的增量等于梁端压力的增量,可得下式[12]:
式中:up为预应力筋伸长量;δb为预应力筋合力增大引起梁的压缩变形;kpt为预应力筋刚度,kpt=ApEp/Lpu,Ap为预应力筋面积,Ep为预应力筋弹性模量;kb为梁构件刚度, kb=AbEc/Lb,Ab为梁截面积,Lb为梁长,Ec为混凝土弹性模量。
则预应力筋合力P为:
其中,Pbi是预应力筋初始合力。
将式(34)代入式(35)中,可得:
图12给出预应力筋合力P的计算值与实测值的对比,两者较吻合,最大误差仅为7.47%。
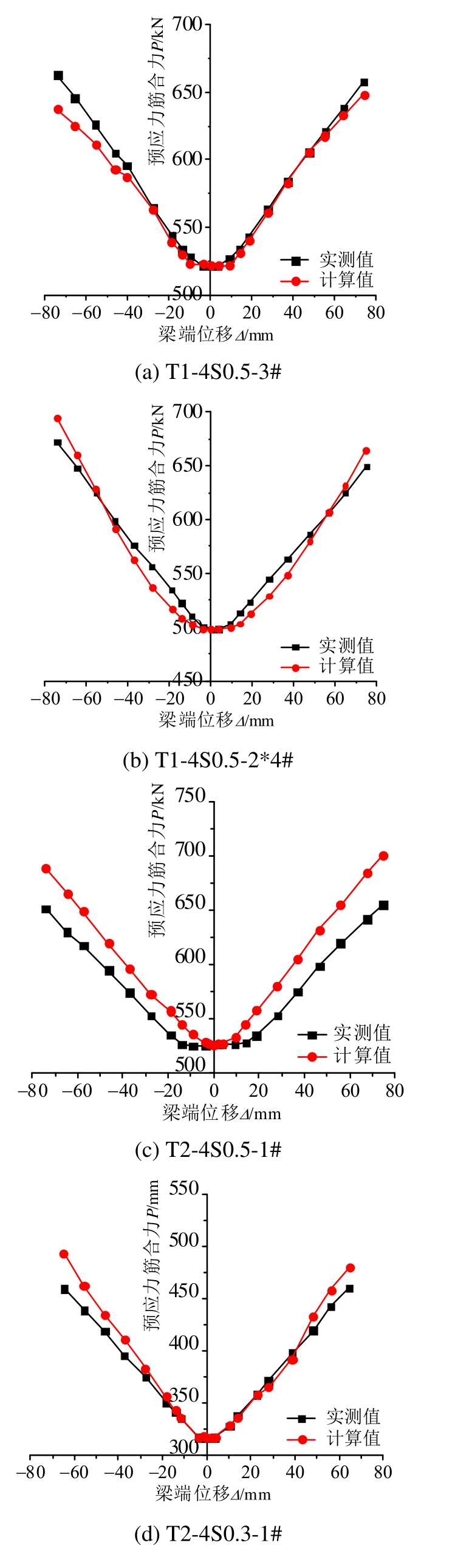
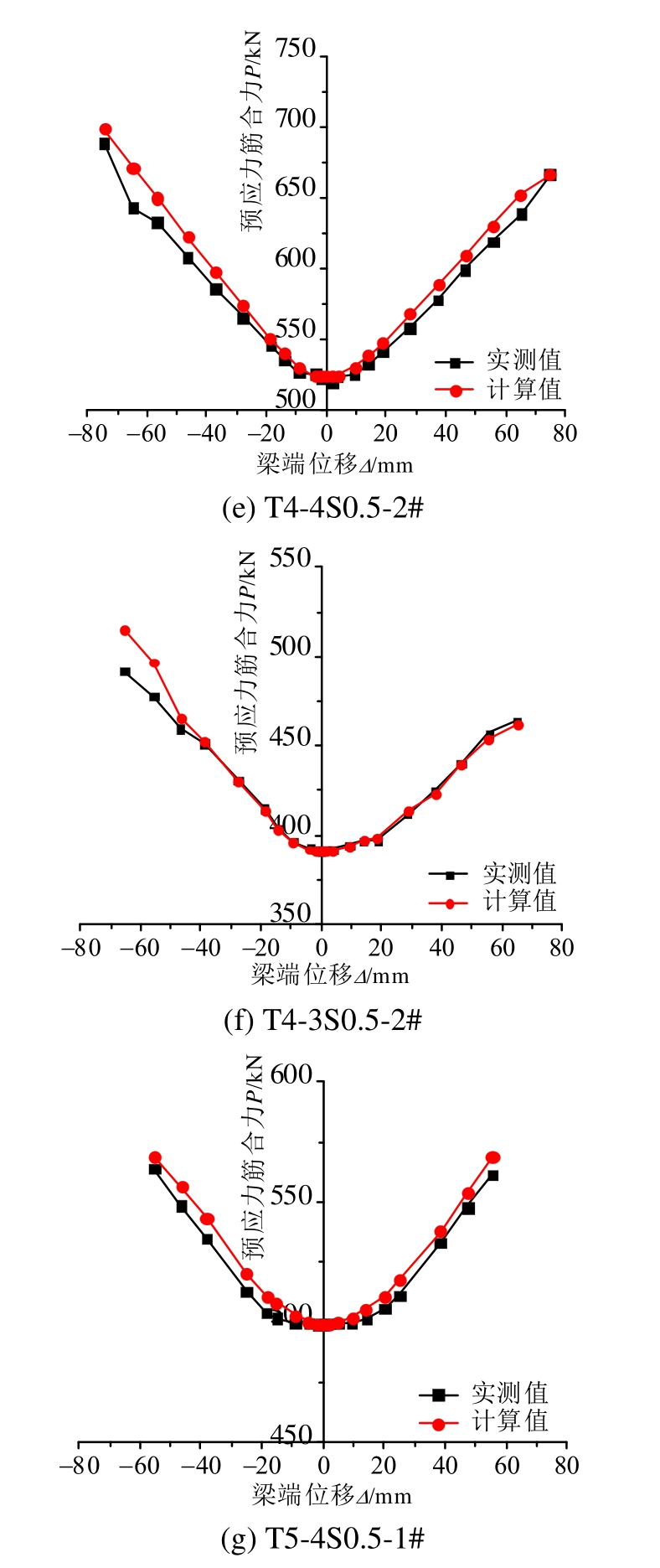
图12 预应力筋合力实测值与理论值的比较
Fig.12 The comparisons of calculated and experimental prestressing forces
3.3 恢复力滞回模型与试验结果的对比
图 13为建立的恢复力滞回模型与试验结果的对比,从图 13可以看出,两者的骨架曲线及加、卸载刚度与试验结果较为接近。
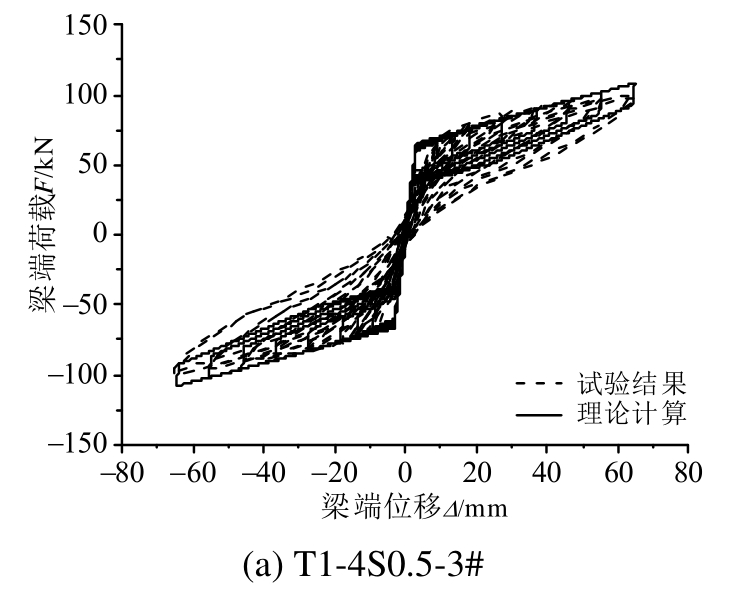
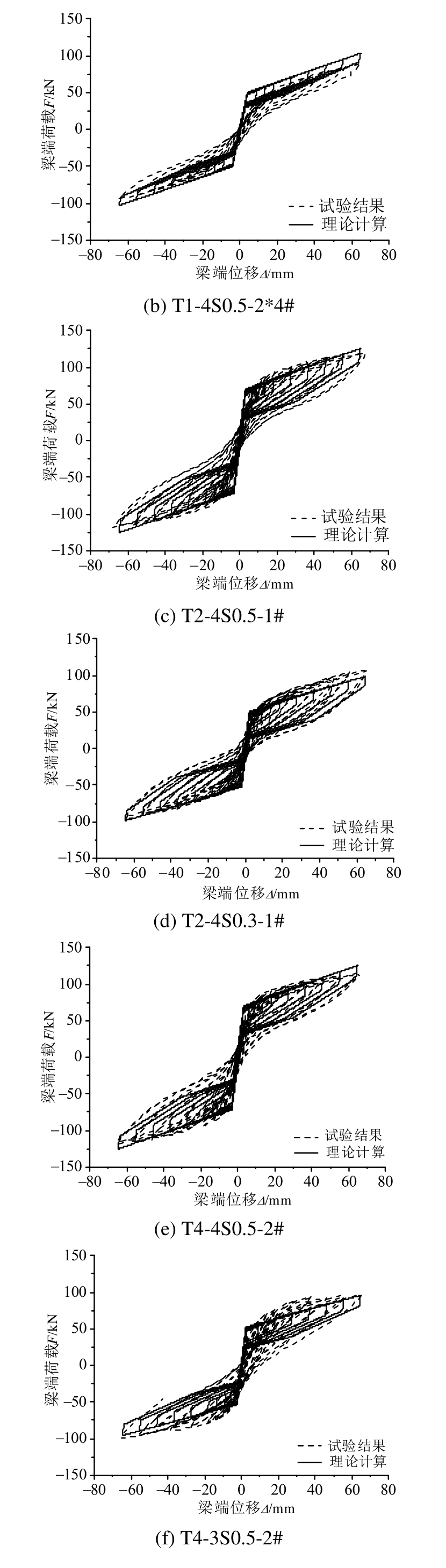
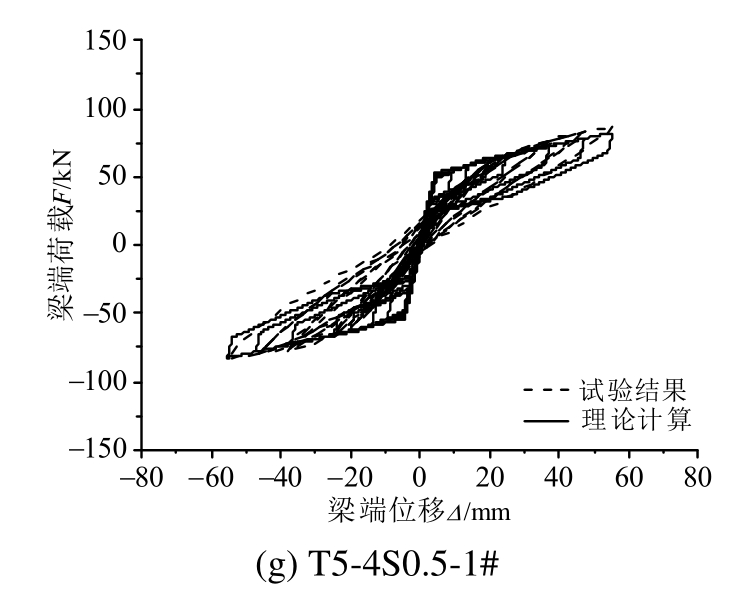
图13 恢复力滞回模型与试验结果的对比
Fig.13 The comparisons of calculated and experimental hysteretic curves
3.4 耗能能力的对比
能量耗散系数E可由下式计算得到:
式中:S(ABC+CDA)为滞回环的面积(见图14阴影部分);S(OBE+ODG)为三角形OBE和三角形ODG面积之和。
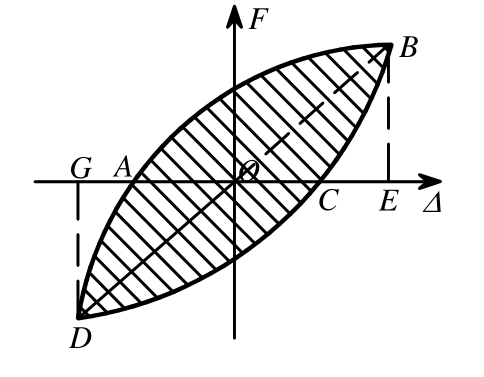
图14 能量耗散系数图
Fig.14 Energy dissipation coefficient
图15、图16分别给出恢复力滞回模型的耗散能量(滞回环的面积)及能量耗散系数的计算值与试验值的对比,其中Ac/At为耗散能量的理论计算值与试验值之比,Ec/Et为能量耗散系数的理论计算值与试验值之比,Ac/At的平均值为 0.947,标准差为0.150,Ec/Et的平均值为0.971,标准差为0.124。随着加载位移的增大两个比值越来越接近 1,理论计算值与试验值较吻合。
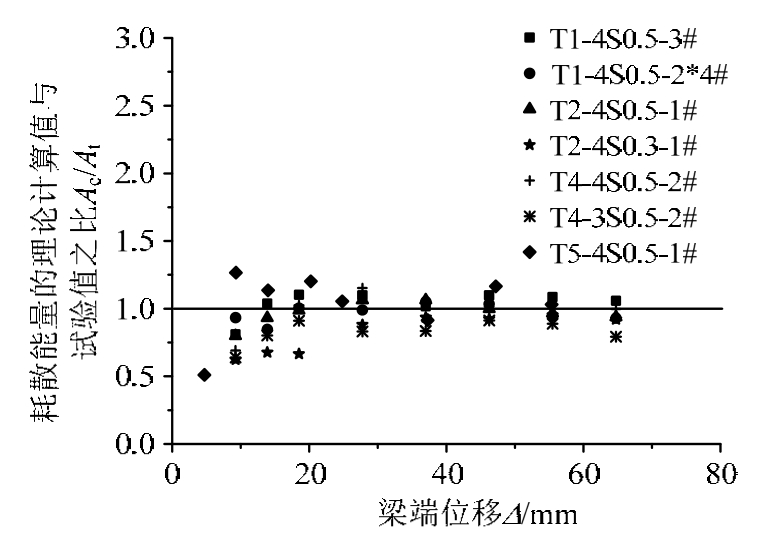
图15 耗散能量的计算值与试验值比较
Fig.15 The comparisons of calculated and experimental dissipated energy
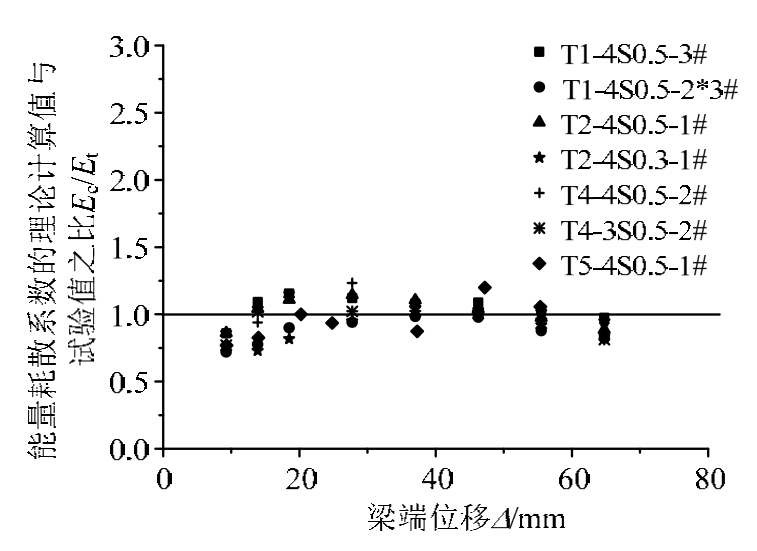
图16 能量耗散系数的计算值与试验值比较
Fig.16 The comparisons of calculated and experimental energy dissipation coefficient
4 结论
针对7个PTED节点的低周往复荷载试验,研究其恢复力模型,得到下列结论:
(1) 确定PTED节点的骨架曲线为三折线模型,给出确定骨架曲线关键特征点对应的荷载及位移的计算方法及步骤。
(2) PTED节点恢复力模型呈旗形,具有良好的自复位能力的同时还具有一定的耗能能力,基于叠加原理,确定PTED节点恢复力模型的滞回规则。
(3) 预应力筋合力的理论计算值与试验值吻合较好,最大误差仅为7.47%。
(4) PTED节点的恢复力滞回模型与试验结果较接近,能综合反映实际节点的骨架曲线、滞回规则以及耗能能力,本文建议的恢复力滞回模型为PTED节点和结构的弹塑性分析提供了依据。
参考文献:
[1]柳炳康, 黄慎江, 宋满荣, 等. 预压装配式预应力混凝土框架抗震性能试验研究[J]. 土木工程学报, 2011,44(11): 1―8.Liu Bingkang, Huang Shenjiang, Song Manrong, et al.Experimental study of seismic performance of prestressed fabricated PC frames [J]. China Civil Engineering Journal, 2011, 44(11): 1―8. (in Chinese)
[2]董挺峰, 李振宝, 周锡元, 等. 无黏结预应力装配式框架内节点抗震性能研究[J]. 北京工业大学学报, 2006,32(2): 144―148.Dong Tingfeng, Li Zhenbao, Zhou Xiyuan, et al.Experimental study on seismic performances of precast prestressed concrete beam-to-column connections with unbonded tendons [J]. Journal of Beijing University of Technology, 2006, 32(2): 144―148. (in Chinese)
[3]GuoTong, Song-Lianglong, Cao-Zhiliang, et al.Large-scale tests on cyclic behavior of self-centering prestressed concrete frames [J]. ACI Structural Journal,2016, 113(6): 1263―1274.
[4]Maurya A, Eatherton MR. Experimental study of the restoring force mechanism in the self-centering beam [J].Frontiers of Structural and Civil Engineering, 2016,10(3): 272―282.
[5]Erochko J, Christopoulos C, Tremblay R, et al. Design,testing, and detailed component modeling of a high-capacity self-centering energy-dissipative brace [J].Journal of Structural Engineering, 2015, 141(8): 1―13.
[6]蔡小宁, 孟少平, 孙巍巍. 自复位预制框架边节点抗震性能试验研究[J]. 土木工程学报, 2012, 45(12): 29―37.Cai Xiaoning, Meng Shaoping, Sun Weiwei.Experimental study on behaviors of beam-column connections for self-centering post-tensioned precast frame [J]. China Civil Engineering Journal, 2012, 45(12):29―37. (in Chinese)
[7]Qiang Shen. Seismic analysis, behavior and design of unbounded post-tensioned hybrid coupled wall structures[D]. Indiana: University of Notre Dame, 2006.
[8]El-Sheikh M, Pessiki S, Sause R, et al. Moment rotation behavior of unbonded post-tensioned precast concrete beam-column connections [J]. ACI Structural Journal,2000, 97(1): 122―131.
[9]蔡小宁, 孟少平. 预应力自复位混凝土框架节点抗震性能数值模拟[J]. 工程力学, 2016, 33(3): 143―151.Cai Xiaoning, Meng Shaoping. Numerical analysis for seismic behavior of self-centering post-tensioned precast beam-to-column connections [J]. Engineering Mechanics, 2016, 33(3): 143―151. (in Chinese)
[10]Brad Weldon, Yahya C Kurama. Nonlinear behavior of precast concrete coupling beams under lateral loads [J].Journal of Structural Engineering, 2007, 133(11): 1571―1581.
[11]蔡小宁, 孟少平, 孙巍巍. 自复位预制框架边节点组件受力性能试验研究[J]. 工程力学, 2014, 31(3): 160―167.Cai Xiaoning, Meng Shaoping, Sun Weiwei.Experimental study on performance of components of the exterior self-centering post-tensioned precast connections[J]. Engineering Mechanics, 2014, 31(3): 160―167. (in Chinese)
[12]Maria M Garlock, Richard Sause, James M Ricles.Behavior and design of posttensioned steel frame systems [J]. Journal of Structural Engineering, 2007,133(3): 389―399.