在我国，RC框架被广泛应用于多层建筑结构，而RC框架梁是框架结构中主要的受力构件。因此，研究RC框架梁在地震作用下的受力特性显得尤其重要。国内外学者对RC框架梁的受力特性进行了诸多研究，郑山锁和杨威等[1]进行了人工气候环境下锈蚀RC框架梁抗震性能试验，其成果为锈蚀RC框架梁抗震性能的分析和数值建模提供了理论依据。周定松和吕西林等[2]进行了 RC框架梁变形能力及基于性能的抗震设计方法研究，并给出了 RC框架梁基于性能抗震设计的一般方法。朱志达等[3]研究了低周反复循环荷载作用下RC框架梁端抗震性能。王子胜[4]、曹大富[5]、杜晓雷[6]等研究了在冻融环境下RC框架梁的抗震性能，并提出了考虑冻融损伤的框架梁恢复力模型。
考虑到地震作用的随机性以及强余震、多次地震作用下结构构件的地震作用效应有所不同，国内外一些学者研究了不同加载制度对RC构件与结构抗震性能的影响：杨晓明等[7]分别采用6种不同加载制度，进行了RC框架柱抗震性能试验研究，得出不同加载制度对 RC框架柱抗震性能有较大影响。史庆轩等[8]研究了加载制度对新型型钢钢筋混凝土柱抗震性能的影响。Anderson[9]进行了不同加载制度下RC框架节点的抗震性能试验，得出当应变超过某一临界应变后，节点抗震性能的退化与加载制度有关。Ranf等[10]对轻微约束RC柱进行了不同加载制度下的抗震性能试验，得出加载制度会对RC柱的破坏形态产生影响。Goodnight等[11]研究了加载历程对RC桥墩抗震性能的影响。基于以上研究，本文依托西安建筑科技大学结构与抗震教育部实验室，补充进行了4种不同加载制度下RC框架梁的拟静力试验研究，以为综合建模分析不同形式地震作用下RC框架结构的抗震性能提供理论依据和试验数据。
1 试验研究方案
1.1 试件设计与制作
本试验参考《高层建筑混凝土结构技术规程》[12]，设计了4榀几何与材料参数相同的RC框架梁(λ=5)，截面尺寸均为 150 mm×250 mm，高度为 1300 mm，受拉和受压纵筋均采用 3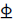
16，配筋率均为1.6%，箍筋为φ6@60。试件模板配筋如图1所示。
采用P.O 42.5R水泥配制强度等级C30的混凝土，配合比为水泥∶水∶天然中砂∶碎石=390∶120∶885∶890，浇筑RC框架梁的同时，制作若干150 mm×150 mm×150 mm的标准立方体试块，用于抗压强度测试。材性试验结果：混凝土轴心抗压强度平均值为20.56 MPa，弹性模量为3.0×104MPa，钢筋力学性能见表1。
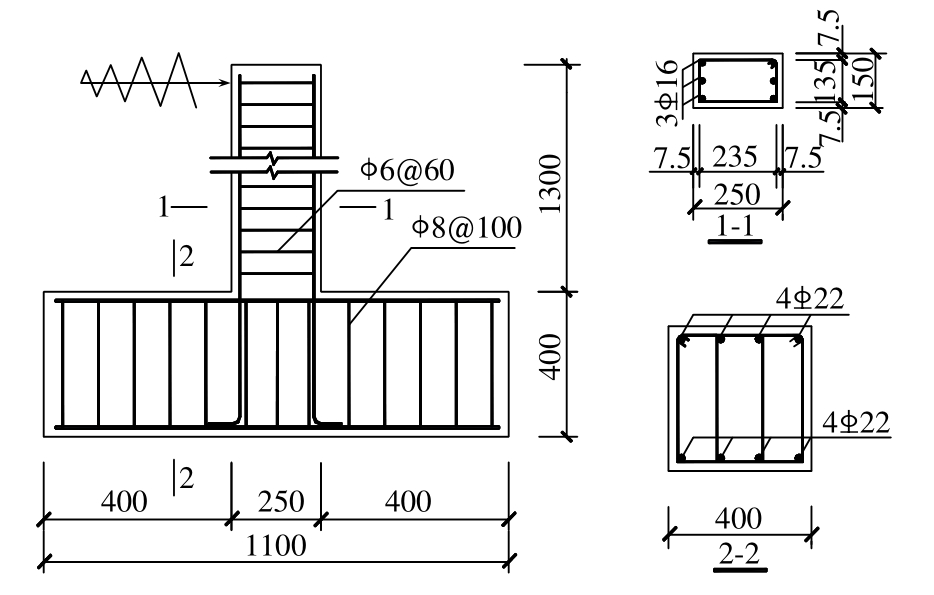
图1 试件尺寸及配筋
Fig.1 Dimensions and reinforcements of specimens
表1 钢筋力学性能
Table 1 Mechanical properties of reinforcement
1.2 试验加载装置和制度
本试验采用位移控制加载，加载装置如图2所示，各试件具体加载制度见表2和图3。其中，B1作为正常加载试件，其加载制度为：在框架梁达到屈服状态之前，选取较小水平位移级差进行加载，以较为准确的获得框架梁开裂、屈服时的水平荷载与位移特征值；框架梁加载至屈服状态后，以屈服时水平位移的倍数为级差进行加载；每级控制位移循环3次；当框架梁水平承载力下降至水平峰值荷载的 85%之后或框架梁破坏明显而不能继续承受竖向荷载时停止试验。
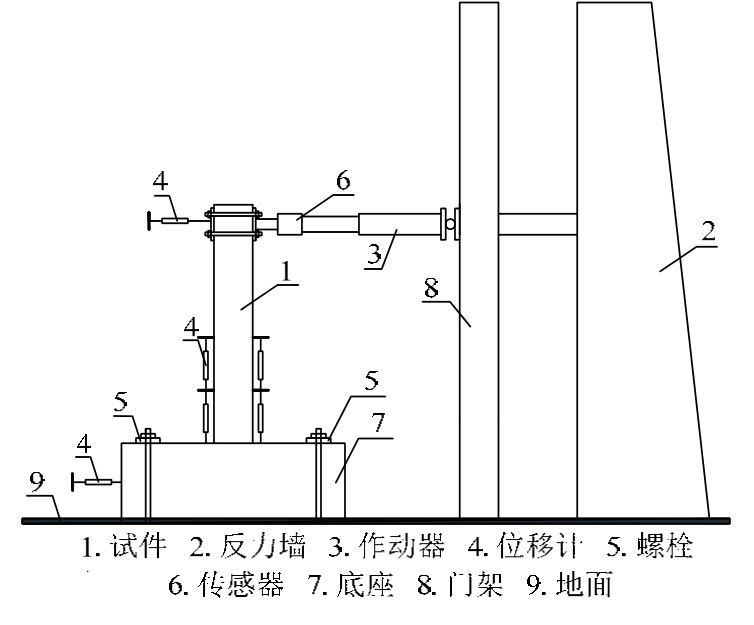
图2 试验加载装置
Fig.2 Experimental equipment for cycle loading
表2 试件加载制度
Table 2 Loading process of specimens
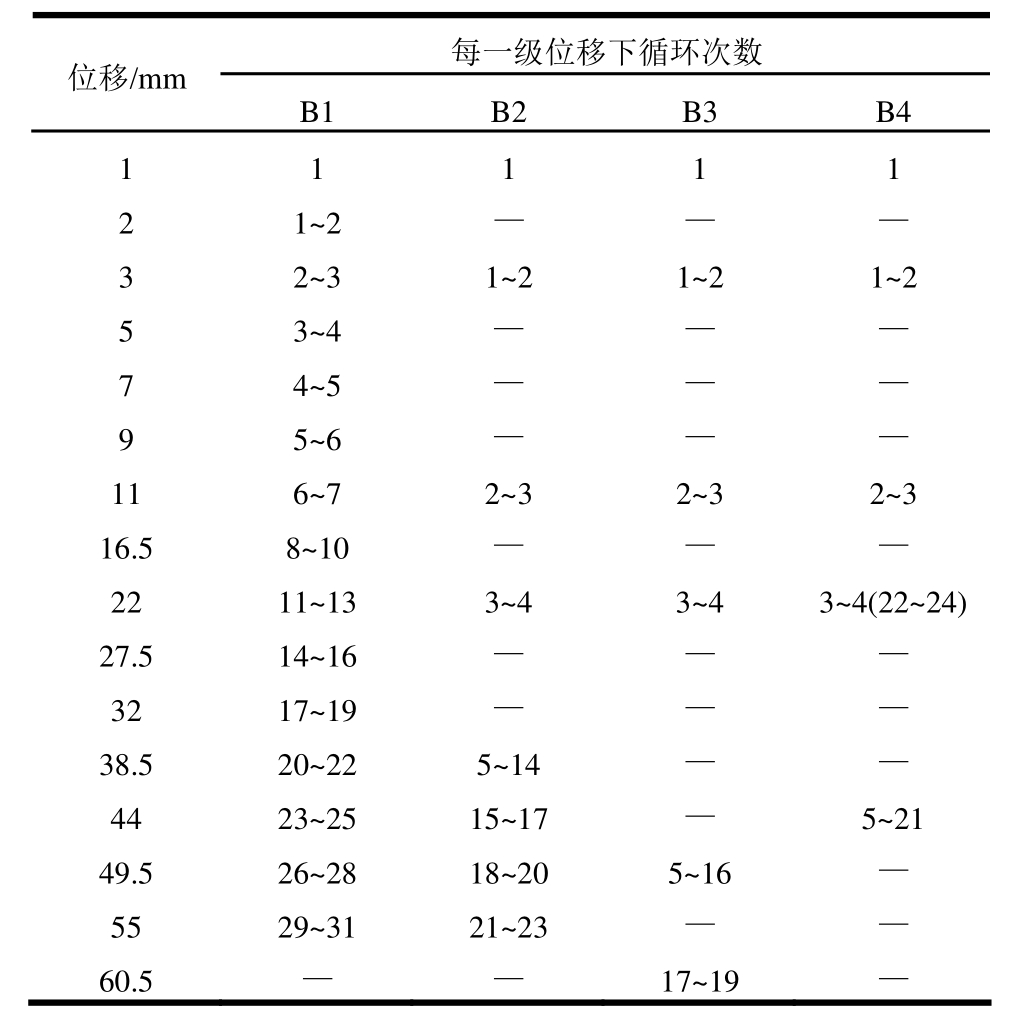
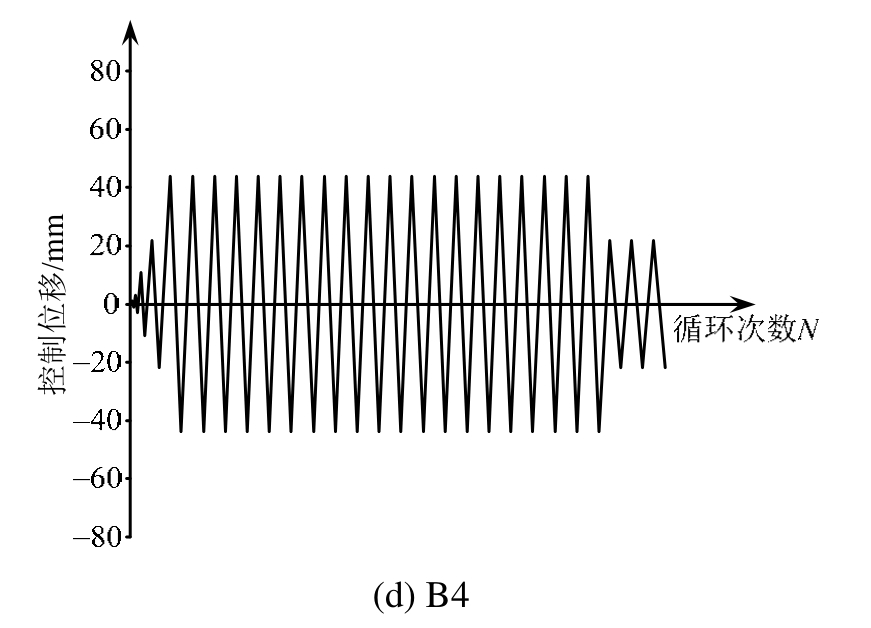
图3 试件加载制度
Fig.3 Loading process of specimens
B2、B3、B4作为不同加载制度对比试件，以揭示不同加载方式对RC框架梁抗震性能的影响。在水平位移达到2Δy(22 mm)之前，B2、B3、B4加载方式相同，之后，加载方式发生较大变化。B2在水平位移幅值为3.5Δy(38.5 mm)处循环了10次，之后每级水平位移循环3次，直至框架梁破坏，以揭示屈服后较小水平位移幅值下多次循环对RC框架梁抗震性能的影响；B3在水平位移幅值为4.5Δy(49.5 mm)处循环12次，之后再加一级水平位移循环3次，试件发生破坏，以揭示屈服后较大水平位移幅值下多次循环对RC框架梁抗震性能的影响；B4在水平位移幅值为4Δy(44 mm)处循环17次，然后返回水平位移幅值2Δy(22 mm)处循环3次，框架梁发生破坏，以揭示屈服后较大再较小水平位移幅值下多次循环对RC框架梁抗震性能的影响。
2 试验结果及分析
2.1 试件的裂缝发展及破坏形态
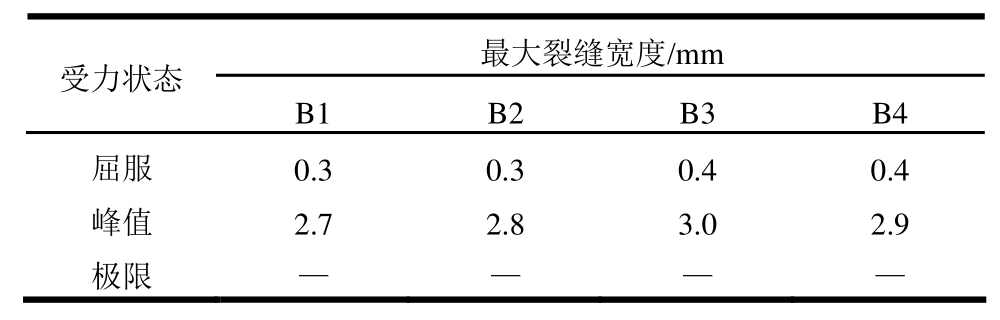
表3为诸试件在不同受力状态时的最大裂缝宽度测试结果，图4为试件最终破坏状态。各试件的裂缝发展过程和破坏状态描述如下。
正常加载制度试件 B1：当水平位移为+2 mm时，在距梁端部约100 mm处出现第一条水平裂缝，试件进入弹塑性开裂阶段；随着水平位移的增大，梁端水平裂缝逐渐增多。当控制位移达到+11 mm时(滞回曲线的屈服点)，基本不再出现新裂缝，此时梁端水平裂缝较多、斜裂缝较少，梁端最大水平裂缝宽度约为 0.3 mm；当控制位移达到+16.5 mm时，梁端水平裂缝加宽，混凝土开始剥落；控制位移为+22 mm时，梁端水平裂缝继续加宽，约为0.8 mm，主要水平裂缝呈贯通趋势；控制位移达到+38.5 mm时，梁端角部混凝土开始压碎，混凝土剥落较严重；控制位移达到+44 mm(滞回曲线峰值点)时，梁端角部混凝土严重压碎、剥落，钢筋外露，梁端最大水平裂缝宽度约为2.7 mm；加载后期，塑性铰区混凝土保护层大面积脱落，纵筋屈曲，框架梁宣告破坏，其破坏形态呈以弯曲变形为主的弯剪破坏，延性较好。
屈服后较小水平位移幅值下多次循环加载试件B2：其裂缝发展过程、破坏形态与B1相似，框架梁破坏形态仍呈以变形为主的弯剪破坏，其剪切变形成分较B1稍有增多。
屈服后较大水平位移幅值多次循环加载试件B3：在控制位移达到+22 mm之前，梁端水平裂缝的发展趋势与 B1基本一致；当控制位移达到+49.5 mm时(滞回曲线峰值点)，梁端塑性铰区形成交叉斜裂缝，且梁端贯通的水平裂缝宽度加宽，梁端角部混凝土压碎，钢筋外露，随着循环次数的增多，框架梁水平承载力下降逐步加快，梁端最大水平裂缝宽度约为3.0 mm；加载后期，尤其是框架梁破坏时，梁端斜裂缝发展明显，剪切变形占很大比例，主要是由于峰值位移出现得早，改变了框架梁的破坏形态，这与文献[10]中的所得结论一致。
屈服后较大再较小水平位移幅值下多次循环试件B4：其裂缝发展过程、破坏形态与B3相似，框架梁破坏时剪切变形成分占更大比例。
对比B1与B2可以发现，试件B2的裂缝发展和破坏形态与B1基本一致，均呈以弯曲变形为主的弯剪破坏，表明屈服后较小水平位移幅值下多次循环的加载制度对 RC框架梁破坏形态基本无影响。
对比B1与B3可以发现，试件B3的裂缝发展和破坏形态变化较大，框架梁破坏时剪切变形的成分占较大比例，表明屈服后较大水平位移幅值下多次循环的加载制度将会因峰值位移出现的早而改变RC框架梁的破坏形态。
对比试件B3与B4可以发现，试件B3与B4裂缝的发展和破坏形态比较接近，表明屈服后经历较大水平位移幅值多次循环后再经较小水平位移幅值多次循环的加载制度对RC框架梁的破坏形态影响不大，其原因是经历较大水平位移幅值多次循环后，RC框架梁已损伤累积较大，再经较小水平位移幅值多次循环加载时其破坏形态将基本维持现状。
对比各试件的最大裂缝宽度发现：峰值位移出现的越早，RC框架梁达到屈服和峰值荷载时的最大裂缝宽度越宽。
表3 试件最大裂缝宽度测试结果
Table 3 Maximum crack width of specimens
注：极限状态时各试件已严重破坏，裂缝开展很大，不再作比较。
图4 试件裂缝分布和破坏状态
Fig.4 Crack distribution and failure patterns of specimens
2.2 滞回曲线
根据试验测得 4榀试件的P-Δ滞回曲线，如图 5所示。分析可知，不同加载制度下RC框架梁的滞回曲线具有如下特点：
1) 正常加载制度试件B1：在达峰值位移之前，同一位移幅值下，随循环次数增加水平荷载略有降低；在达峰值位移之后，随着循环次数的增加，水平荷载明显下降，且位移幅值越大水平荷载随着循环次数下降越快。
2) 试件B2与B3和B4相比，在屈服后的不同水平位移幅值控制加载中，随着循环次数增多，B2水平荷载下降较慢，而B3和B4水平荷载下降较快。表明屈服后较小水平位移幅值下循环次数对框架梁水平承载力的降低影响不大，而较大水平位移幅值下循环次数对框架梁水平承载力的降低影响明显。
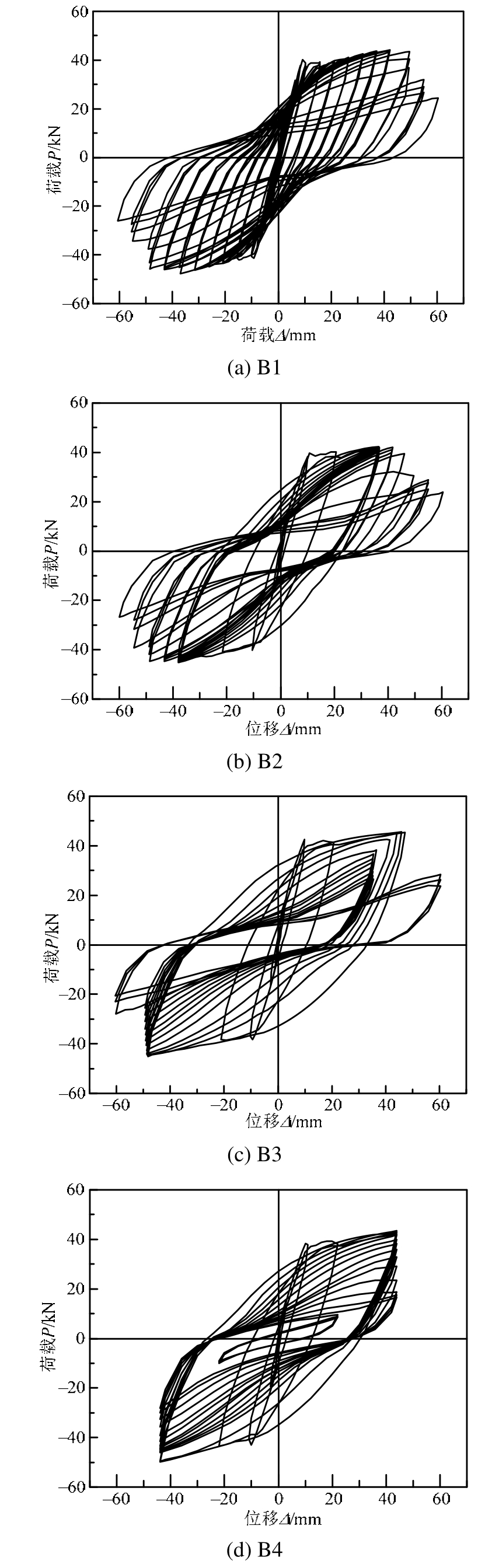
图5 试件的滞回曲线
Fig.5 Hysteretic curves of specimens
2.3 骨架曲线及特征参数
基于滞回曲线绘出各试件的骨架曲线，如图 6所示。本文采用“能量等值法”确定试件骨架曲线的屈服点，取峰值荷载下降85%的值为极限荷载，极限位移为对应于极限荷载的位移。以延性系数μ来表征RC框架梁的延性性能，计算公式如下[13]：
式中，uΔ、yΔ分别为试件的极限位移和屈服位移。
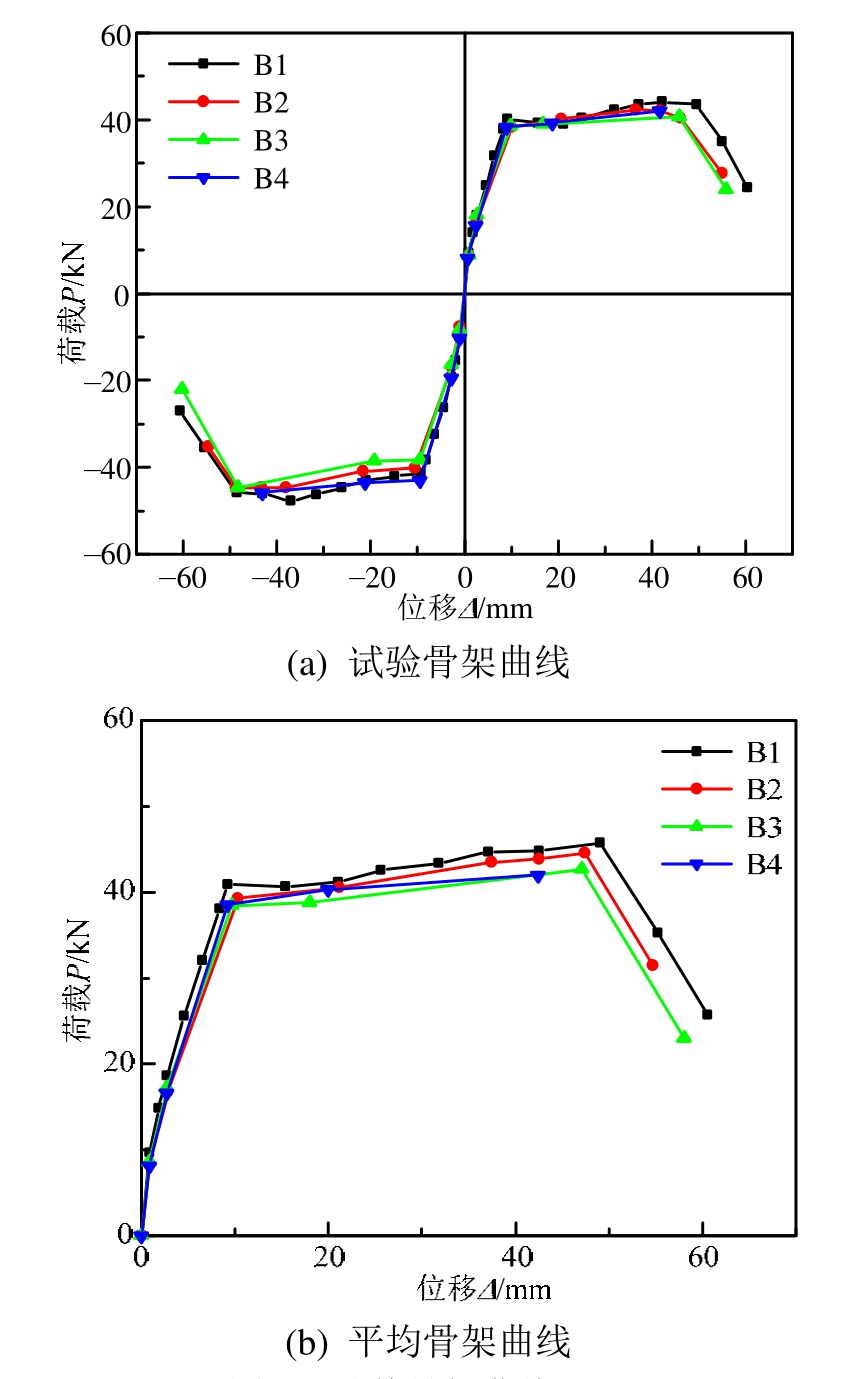
图6 试件骨架曲线对比
Fig.6 Comparison of skeleton curves of specimens
各 RC框架梁试件的屈服荷载(Py)、屈服位移(Δy)、峰值荷载(Pc)、峰值位移(Δc)、极限荷载(Pu)、极限位移(Δu)、延性系数(μ)计算结果见表 4。
表4 试件特征参数
Table 4 Parameters of specimens
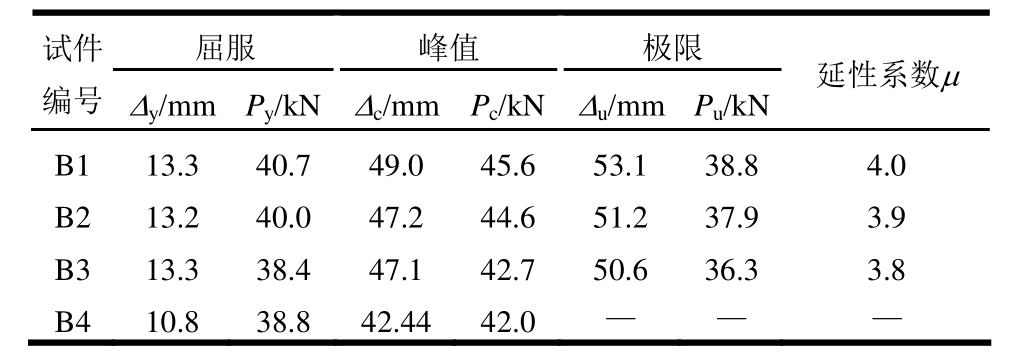
注：B4屈服后采用较大再较小水平位移控制加载，故不计算B4的极限荷载和位移，同样骨架曲线也没有软化段。
由图5和表4可知：
1) 不同加载制度下各试件的屈服荷载、峰值荷载和极限荷载变化不大：峰值荷载之前，骨架曲线基本重合，表明在达到峰值荷载之前，加载制度对框架梁的承载力影响不大。峰值之后，框架梁承载力随加载制度的变化表现出不同下降趋势，其中试件B3承载力下降速度大于试件B1，试件B2介于二者之间，说明峰值位移出现的越早，软化段的承载力下降越快。
2) 由于加载制度的不同，各试件的延性系数有所不同，变化规律是：峰值位移出现早的框架梁，其延性系数较低，变形能力较差。
2.4 塑性转角和塑性铰高度
分别采用文献[13]和文献[14]中公式来计算塑性铰区的转角pθ，公式如下：
式中：uΔ、yΔ分别为试件的极限位移和屈服位移；L为试件的计算高度；1δ、2δ分别为塑性铰受拉侧与受压侧的伸长量与压缩量，h为框架梁截面的高度。不同加载制度下各试件塑性铰转角和高度见表 5。
表5 试件的塑性铰转角和高度
Table 5 Rotational angles and height of plastic hinge of specimens
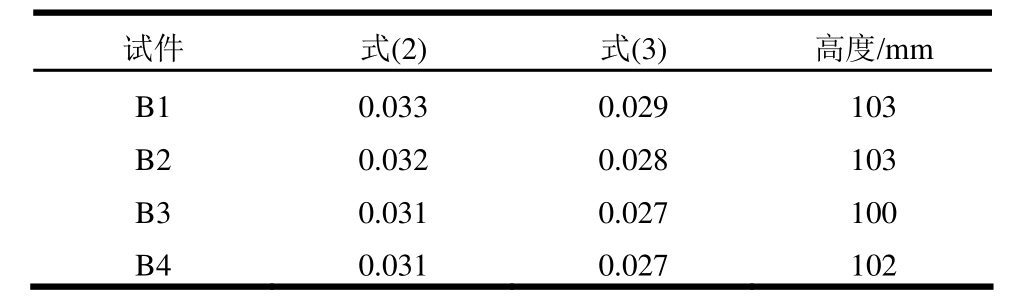
由表5可知，不同加载制度下各试件的塑性铰转角不同，主要表现在：峰值位移出现早的试件塑性转角较低，变形能力较差。文献[13]塑性转角计算值较文献[14]偏大，主要是由于其计算塑性转角时包含了框架梁端剪切变形所引起的梁顶水平位移。但不同加载制度下塑性铰的高度基本没有变化，说明加载制度对塑性铰高度没有影响。
2.5 刚度退化和强度衰减
由图6骨架曲线可以看出，在达到峰值荷载之前，框架梁在不同加载制度下的刚度和强度退化变化不大，而在峰值荷载之后的软化段其刚度和强度发生不同程度的退化。由于框架梁在软化段的抗震性能对结构的抗倒塌能力至关重要，以下着重探讨框架梁在软化段的刚度和强度退化规律。
取骨架曲线软化段每级水平位移幅值循环下，推拉方向荷载绝对值之和与位移绝对值之和的比值，为每次循环下的割线刚度K；其与框架梁每级位移幅值第一次循环的割线刚度K0的比值Ki/K0为试件刚度退化系数。由试验数据分析得到不同加载制度下框架梁试件刚度退化关系曲线，如图 7所示。
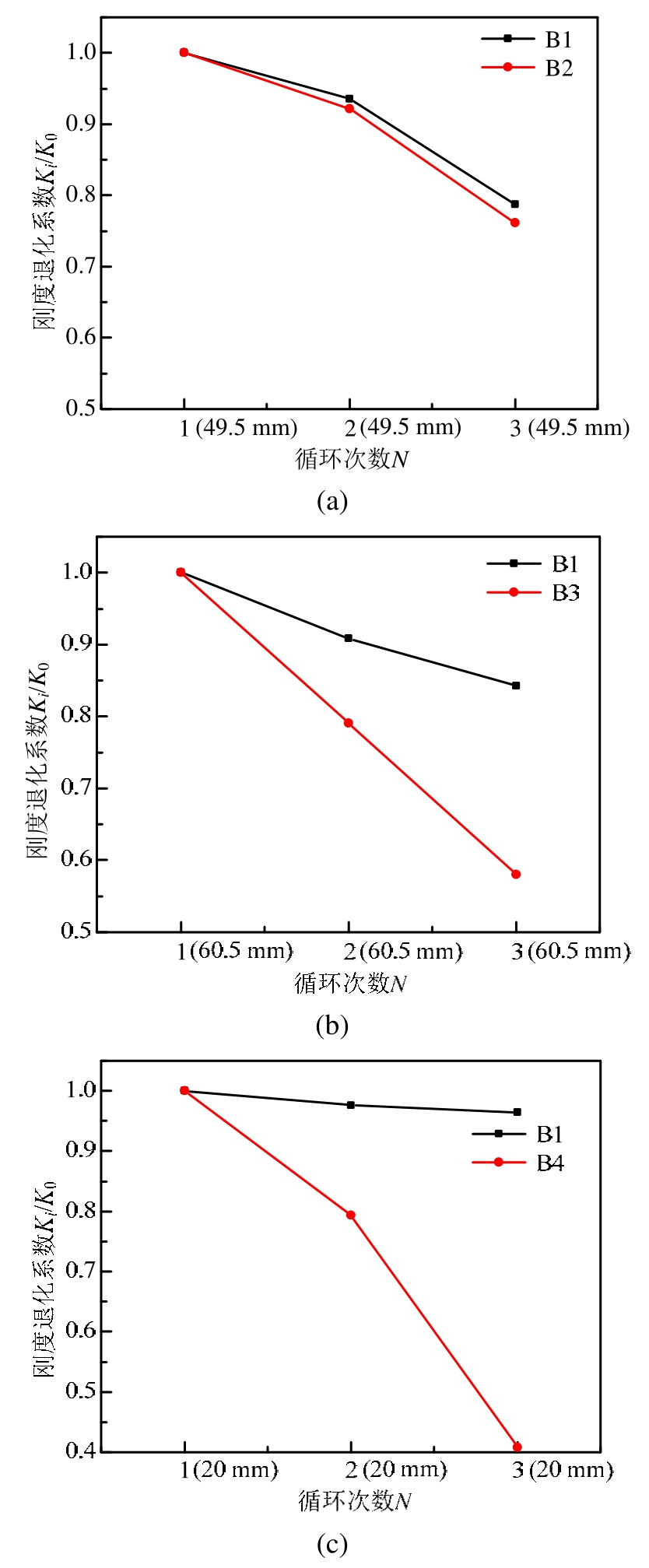
图7 试件刚度退化规律
Fig.7 Stiffness degradation law of specimens
根据各试件在同级水平控制位移下的刚度退化规律可得出以下结论：
1) 图7(a)为试件B1和B2在水平控制位移幅值为49.5 mm的3次循环加载中的刚度退化规律。可以看出，屈服后较小水平位移幅值下多次循环加载试件 B2比正常加载试件 B1的刚度退化略有加快，但刚度退化系数降低的幅度较小，约为 5%。说明屈服后较小水平位移幅值下多次循环加载对框架梁软化段刚度退化的影响较小。
2) 图7(b)为试件B1和B3在水平控制位移幅值为60.5 mm的3次循环加载中的刚度退化规律。可以看出，屈服后较大水平位移幅值下多次循环加载试件B3比正常加载试件B1的刚度退化加快，且刚度退化系数降低的幅度也较大，约为35%。说明屈服后较大水平位移幅值下多次循环加载对框架梁软化段刚度退化的影响较大。
3) 图7(c)为试件B1和B4在水平控制位移幅值为22 mm的3次循环加载中的刚度退化规律。可以看出，屈服后经历较大水平位移幅值多次循环后再经较小水平位移幅值多次循环加载试件B4比正常加载试件B1的刚度退化显著加快，且刚度退化系数降低的幅度很大，约为60%。说明屈服后经历较大水平位移幅值多次循环后再经较小水平位移幅值多次循环加载，框架梁的刚度会显著降低。
同理，由试验数据分析得到不同加载制度下框架梁试件强度衰减关系曲线，如图8所示。
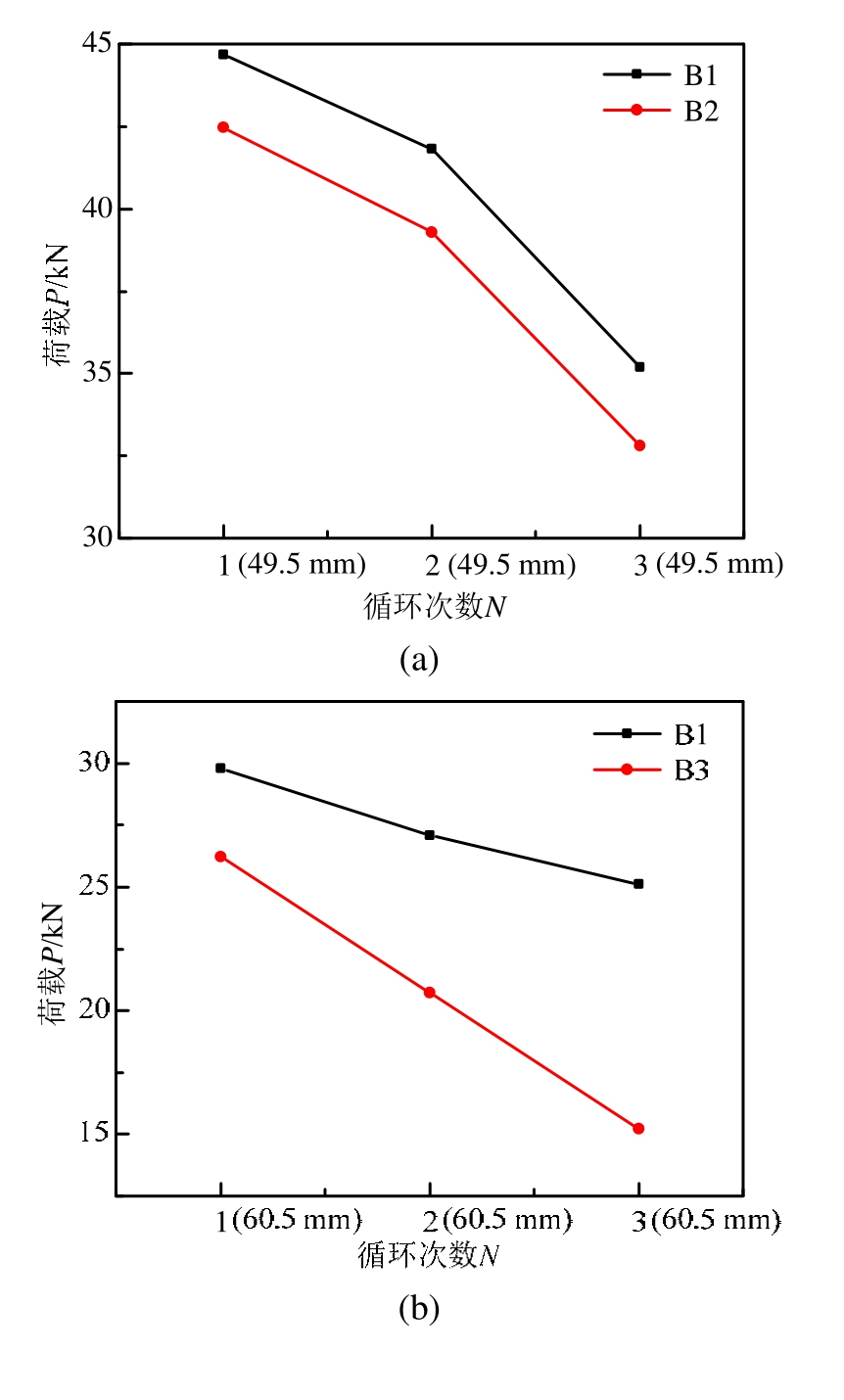
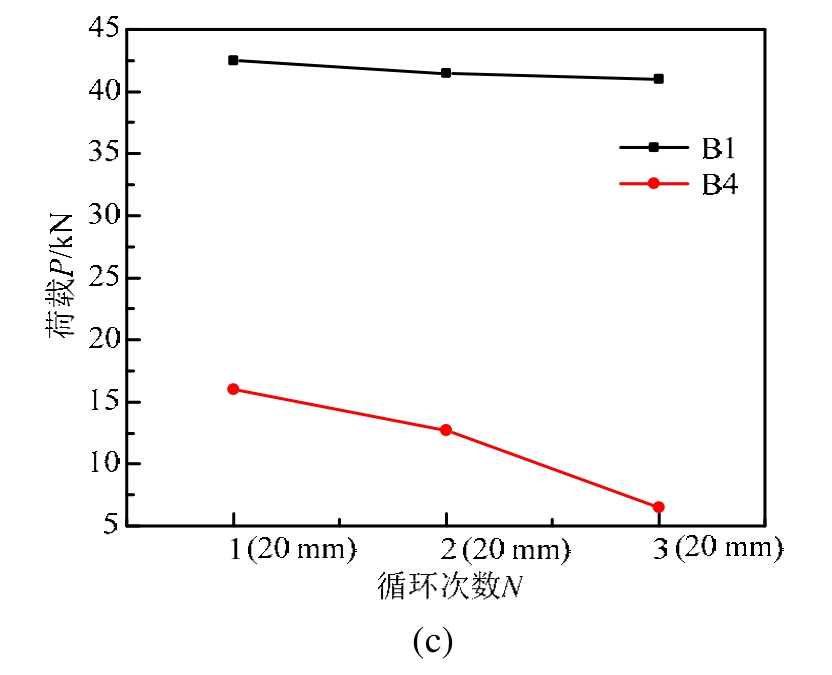
图8 试件强度衰减规律
Fig.8 Strength attenuation law of specimens
根据各试件在同级水平控制位移下的强度衰减规律可得出以下结论：
1) 图8(a)为试件B1和B2在水平控制位移幅值为49.5 mm的3次循环加载中的强度衰减规律。可以看出，屈服后较小水平位移幅值下多次循环加载试件 B2比正常加载试件B1的承载力降低约为5%，曲线的斜率变化较小，说明屈服后较小水平位移幅值下多次循环加载对框架梁软化段强度衰减的影响较小。
2) 图8(b)为试件B1和B3在水平控制位移幅值为60.5 mm的3次循环加载中的强度衰减规律。可以看出，屈服后较大水平位移幅值下多次循环加载试件 B3比正常加载试件 B1的承载力降低约17%，曲线变陡，强度衰减加快。说明屈服后较大水平位移幅值下多次循环加载对框架梁软化段强度衰减的影响较大。
3) 图8(c)为试件B1和B4在水平控制位移幅值为22 mm的3次循环加载中的强度衰减规律。可以看出，屈服后经历较大水平位移幅值多次循环后再经较小水平位移幅值多次循环加载试件B4比正常加载试件B1的承载力降低约62%，且曲线变陡，强度衰减加快。说明屈服后经历较大水平位移幅值多次循环后再经较小水平位移幅值多次循环加载，框架梁的强度会显著降低。
2.6 耗能能力
采用等效粘滞阻尼系数和功比指数来描述不同加载制度对RC框架梁滞回耗能特性的影响。等效粘滞阻尼系数he[15]计算公式如下：
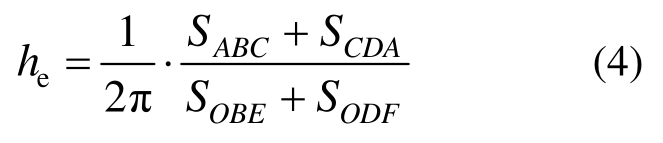
式中：面积 SABC+SCDA为荷载正反交变一周时结构所耗散的能量；SOBE和SODF为理想弹性结构在达到相同位移时所吸收的能量，如图9所示。
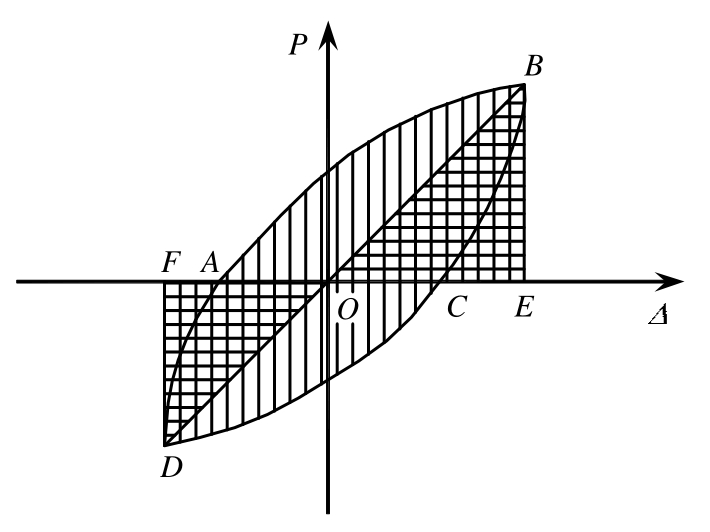
图9 粘滞阻尼系数计算示意图
Fig.9 Calculation diagram of energy dissipation coefficient
功比指数Iw的计算公式如下[15]：
式中：iP、iδ分别为第i次循环时卸载点的荷载和位移值；Py、yδ分别为屈服荷载和屈服位移值。
RC框架梁的粘滞阻尼系数和功比指数计算结果见表 6。此外，本文给出了不同加载制度下 RC框架梁在屈服、峰值和极限状态时累积滞回耗能能力，见图10。
表6 试件耗能性能指标
Table 6 Hysteretic energy dissipation indicators
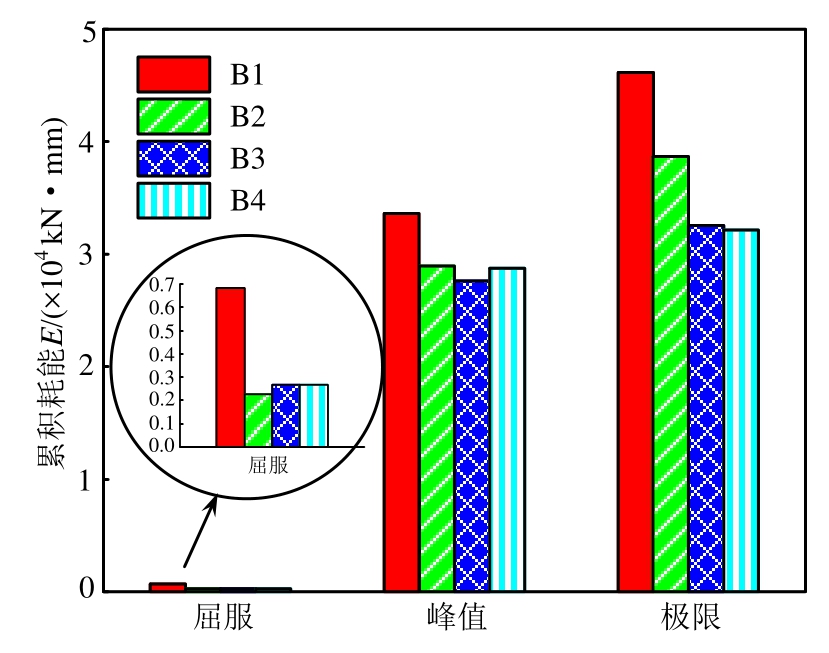
图10 累积耗能
Fig.10 Cumulative energy dissipation
结合表6和图10可知：
1) 对比试件 B1～B3，峰值位移出现的越早，其功比指数越小，峰值和极限状态的粘滞阻尼系数越小，耗能能力变差。
2) 对比不同加载制度下各试件的累积耗能，4榀试件在屈服状态时的耗能能力都很小，但由于B1的加载循环次数较多，所以较其他试件耗能较多；在峰值状态时采用其他加载制度的 B2、B3和 B4耗能能力基本相同，但都比正常加载制度下的 B1耗能能力略低，约为正常加载的85%；在极限状态时，各试件的累积耗能能力差别比较明显：屈服后较小水平位移幅值下多次循环加载试件B2的耗能能力约为正常加载试件B1的82%，屈服后较大水平位移幅值下多次循环加载试件B3和B4的耗能能力约为正常加载试件B1的70%。表明采用不同加载制度对框架梁的累积耗能能力影响较大。
3) 对比试件B3与B4在极限状态时的耗能能力，发现二者基本重合，说明屈服后经历较大水平位移幅值多次循环后再经较小水平位移幅值多次循环加载说明在经历大位移幅值后再反向加载对框架梁的耗能能力影响不大。
3 结论
(1) RC框架梁的破坏形态随加载制度的改变发生不同的变化，主要表现为：峰值位移出现的越早，框架梁破坏时剪切变形成分越大，塑性转角变小，延性变差。
(2) 随着循环位移幅值和循环次数的不同，RC框架梁的刚度、强度退化也有一定差异，表现为：在滞回曲线软化段，经历较大位移幅值循环(或较多次循环)后的框架梁比较小位移幅值循环(或较少次循环)后框架梁的刚度和强度退化快，抗震性能差。
(3) 不同加载制度下，RC框架梁的耗能能力不同。其变化规律为：峰值位移出现的越早的框架梁，其耗能能力越差。
参考文献：
[1]郑山锁, 杨威, 赵彦堂, 等. 人工气候环境下锈蚀 RC弯剪破坏框架梁抗震性能试验研究[J]. 土木工程学报,2015, 48(11): 27―35.Zheng Shansuo, Yang Wei, Zhao Yantang, et al.Experimental research on the seismic behaviors of corroded RC frame beams failed in flexure-shear mode under the artificial climate [J]. China Civil Engineering Journal, 2015, 48(11): 27―35. (in Chinese)
[2]周定松, 吕西林, 蒋欢军. 钢筋混凝土框架梁的变形能力及基于性能的抗震设计方法[J]. 地震工程与工程振动, 2005, 25(4): 60―66.Zhou Dingsong, Lü Xilin, Jiang Huanjun. Deformation capacity and performance-based seismic design method for RC frame beams [J]. Earthquake Engineering and Engineering Vibration, 2005, 25(4): 60―66. (in Chinese)
[3]朱志达, 沈参璜. 在低周反复循环荷载作用下钢筋混凝土框架梁端抗震性能的试验研究(3)[J]. 北京工业大学学报, 1989, 15(1): 81―93.Zhu Zhida, Shen Canhuang. An experimental investigationon earthquake resistant behavior of the beam end of reinforeed conerete framed buildings under low repeated and reversed loading (3) [J]. Journal of Beijing Polyteching University, 1989, 15(1): 81―93. (in Chinese)
[4]王子胜. 冻融环境下RC框架梁抗震性能试验研究[D].西安: 西安建筑科技大学, 2015.Wang Zisheng. Experimental study on seismic performance of RC frame beam under freeze-thaw cycles[D]. Xi’an: Xi’an University of Architecture and Technology, 2015. (in Chinese)
[5]曹大富, 葛文杰, 郭容邑, 等. 冻融循环作用后钢筋混凝土梁受弯性能试验研究[J]. 建筑结构学报, 2014,35(6): 137―144.Cao Dafu, Ge Wenjie, Guo Rongyi, et al. Experimental study on flexural behaviours of RC beams after freeze-thaw cycles [J]. Journal of Building Structures,2014, 35(6): 137―144. (in Chinese)
[6]杜晓雷. 钢筋混凝土梁在冻融循环和锈蚀下的受弯性能研究[D]. 吉林: 吉林大学, 2011.Du Xiaolei. Research on the bending performanee of reinforced conerete beam under the freeze-thaw cyeles and corrosion [D]. Jilin: Jilin University, 2011. (in Chinese)
[7]杨晓明, 丰定国, 杨睿. 不同加载制度下钢筋混凝土柱抗震性能的试验研究[J]. 工业建筑, 2005, 35(9):42―45.Yang Xiaoming, Feng Dingguo, Yang Rui.Experimental study on aseismic performance of RC column under different loading systems [J]. Industrial Construction, 2005, 35(9): 42―45. (in Chinese)
[8]史庆轩, 王朋, 李坤, 郭智峰, 王南, 田建勃. 加载制度对新型型钢混凝土柱的抗震性能影响[J]. 工程力学,2014, 31(3): 152―159.Shi Qingxuan, Wang Peng, Li Kun, Guo Zhifeng,Wang Nan, Tian Jianbo. Infiuence of loading regimes on seismic behavior of new type steel reinforced concrete columns [J]. Engineering Mechanics, 2014, 31(3): 152―159. (in Chinese)
[9]Anderson M, Lehman D, Stanton J. A cyclic shear stress–strain model for joints without transverse reinforcement [J]. Engineering Structures, 2008, 30(4):941―954.
[10]Ranf R T, Eberhard M O, Stanton J F. Effects of displacement history on failure of lightly confined bridge columns [J]. Concrete, 2006, 40(4): 23―42.
[11]Goodnight J, Feng Y, Kowalsky M, et al. The effect of load history on reinforced concrete bridge column behavior [R]. Concrete Structures, 2012: 62―89.
[12]JGJ3-2010, 高层建筑混凝土结构技术规程[S]. 北京:中国建筑工业出版社, 2011.JGJ3-2010, Technical specification for concrete structures of high-rise building [S]. Beijing: China Architecture & Building Press, 2011. (in Chinese)
[13]JGJ101-96, 建筑抗震试验方法规程[S]. 1996.JGJ101-96, Specification of testing methods for earthquake resistant building [S]. 1996. (in Chinese)
[14]李振宝, 解咏平, 杜修力, 等. 单调水平荷载作用下钢筋混凝土柱受弯性能尺寸效应试验研究[J]. 建筑结构学报, 2013, 34(12): 77―85.Li Zhenbao, Xie Yongping, Du Xiuli, et al. Experimental study on size effect of flexural behavior for reinforced concrete columns subjected to monotonic horizontal loading [J]. Journal of Building Structures, 2013, 34(12):77―85. (in Chinese)
[15]姚谦峰, 陈平. 土木工程结构试验[M]. 北京: 中国建筑工业出版社, 2007: 216―223.Yao Qianfeng, Chen Ping. Civil engineering structural experiment [M]. Beijing: China Architecture & Building Press, 2007: 216―223. (in Chinese)