岩石赋存于复杂的地质环境中，具有建造和改造成因的复杂内部结构层次，是非均质材料。斑团状缺陷结构是岩石内部一种常见的非均质结构，其组成可能是坚硬的石英或方解石，或是较软弱的泥质。图1为含团状缺陷结构白云岩照片，其团块组成为方解石。即使取自同一岩块的岩样应力-应变全过程曲线和强度也差别较大；在荷载作用下岩石表现出非连续性、非均质性和各向异性特征[1―3]，是缺陷结构存在导致微破裂聚集和扩展结果，同样被岩石声发射监测所证实[4―5]。该过程引起岩样加载过程中应力场不均匀分布[6]。近年来研究者发现含缺陷岩石加载过程伴随着逆变形的产生应变场同样不均匀[7―8]。应力(应变)场的不均匀分布被认为导致了岩石破坏的局部化现象。实际工程经验同样表明，岩石破坏极少是整体性的同时破坏[9―10]，而是起始于强烈的局部破坏，最早出现的变形带被称为局部化带。刘招伟、李元海[11]对含孔洞岩石试件变形进行研究，表明变形局部化起始于轴向位移的80%处，应力峰值点附近变形局部化最为剧烈。
图1 含斑团状缺陷结构白云岩
Fig.1 Dolomite with block mass
岩石内部缺陷虽然是一种普遍现象，但缺陷导致的微破裂聚集、不均匀应力场形成、及破坏局部化成因等问题仍不清楚。目前对含缺陷结构岩石力学特征研究多集中于静力学，而已有研究发现含缺陷岩石变形及破坏对加载速率有很大依赖关系[12]，表明其力学特性具有动态特征。
岩石内部缺陷具有随机性，从室内试验获得某种规律需要大量试验投入[13]，数值模拟可对理想结构进行构建，并可以方便控制模型力学参数及布置观测任务，越来越受到欢迎。颗粒流是Cundall等[14]于 1979年提出的离散元法，已开发出二维圆盘和三维圆球的颗粒流程序(Particle Flow Code)，并已广泛应用于岩石力学研究中。本文利用颗粒流离散元法和PFC2D程序，建立含团块结构岩石试样，通过对试样进行三轴压缩试验和三轴疲劳试验，分析团块对试样破坏特征、强度和应力-应变分布的影响。
1 PFC2D数值方法及试验方案
1.1 颗粒流离散元法的基本理论
颗粒流离散元法是基于离散元思想认为物质是由一系列离散的、独立运动的颗粒(单元)组成，用来模拟颗粒运动及相互作用的方法[15]。颗粒流离散元法采用中心差分计算法，每个时步迭代计算并遍历所有颗粒的作用力、运动速度、位移和位置。颗粒被视为刚体，颗粒运动及粒间相互作用符合牛顿第二定律和力-位移定律(图2(a))。
PFC2D接触黏结模型(Contact-bond model)允许颗粒间平动或转动，能承受荷载并满足力-位移关系。接触力在接触面上分为法向接触力和切向接触力，其中切向接触力用增量形式给出：
式中，Fin和Fis分别为法向和切向接触力分量，其中：
式中：Un为每时步内法向位移(由于颗粒为刚体，故计算颗粒与颗粒之间的重叠位移量)；ΔUs为每时步内切向位移增量；Kn为法向刚度；Ks为切向刚度，通过两两接触颗粒单元刚度knA、knB计算：
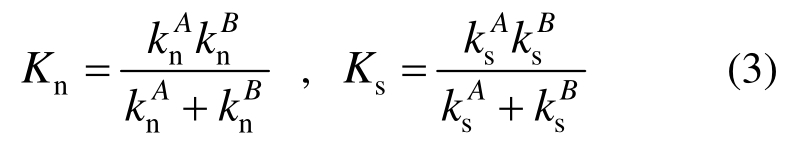
当作用荷载超过黏结强度(法向黏结强度Fn和c切向黏结强度Fcs)时则接触被破坏，破坏后颗粒间可发生滑移，其条件为：
式中，u为颗粒间摩擦系数，并计算下一时步siF：
黏结颗粒模型允许粒间产生由黏接刚度控制的拉、压变形(图 2(b))，同时可产生由黏结强度控制的旋转、剪切破坏(图2(c))。
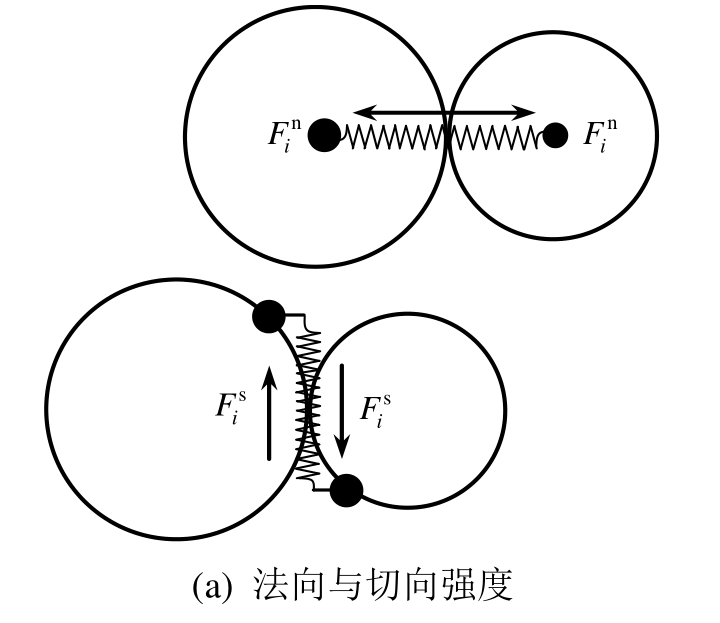
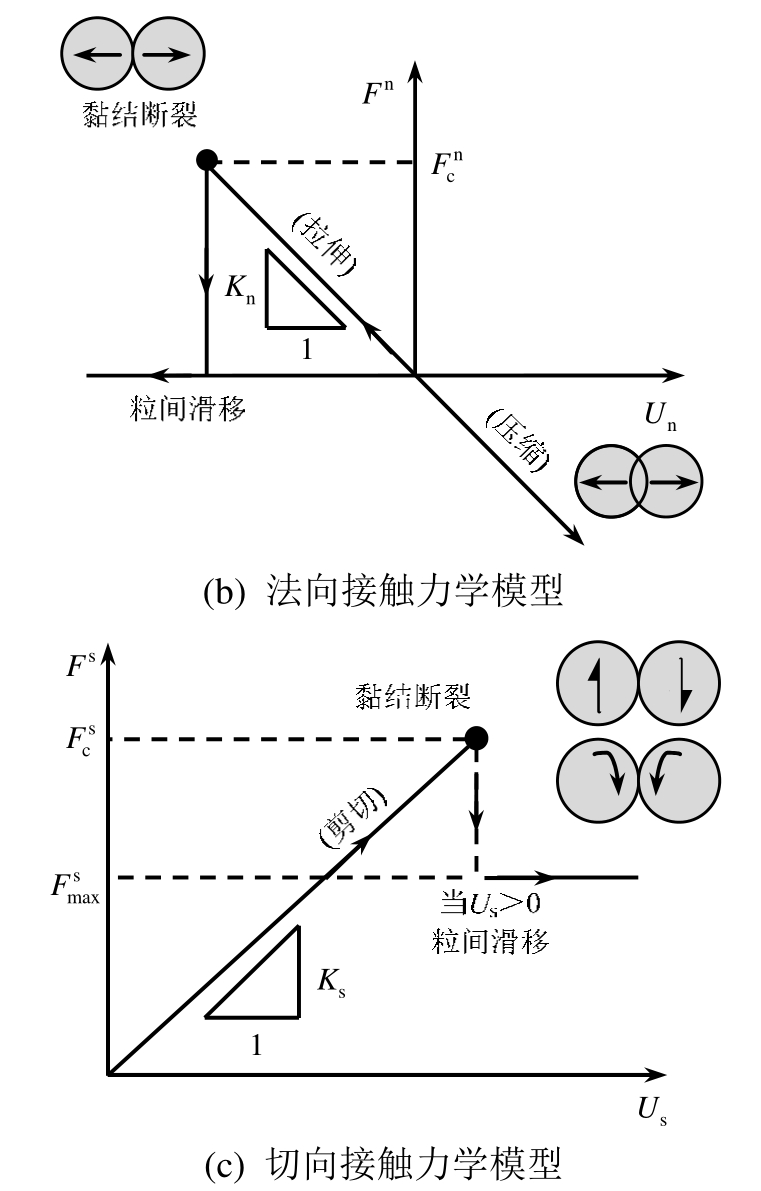
图2 接触黏结模型
Fig.2 Contact-bond model
1.2 模型构建及加载机制
1) 三轴数值模型构建
PFC2D建模过程包括颗粒生成、颗粒属性及粒间黏结本构设置和围压设置等。首先定义由水平(1#、4#)和竖直(2#、3#)刚性墙围成的模型空间，而后将指定数量的颗粒放于模型空间内(图3)，让颗粒膨胀并相互碰撞，通过颗粒最小和最大半径、颗粒密度和孔隙率等参数使颗粒均匀地充满模型空间。在“制样”过程中 PFC可调节组成试样颗粒的级配，进而“配制”出不同力学性质试样。在岩石力学中由于岩石结构不同导致的力学性质差异比较明显，如等粒结晶结构一般比非等粒结晶结构的强度高，在等粒结构中，细粒结晶结构比粗粒的强度高，在斑状结构中，细粒基质比玻璃质强度高[16]。为排出试样不均匀性导致的力学性质差异，单分析团块对试样影响，本文所有数值模型试样均为相同等粒细粒结构，颗粒总数为 4万个，粒径为0.45 mm±0.05 mm。试样颗粒参数见表1，其中ρ为颗粒密度，Rmin为粒径上限，Rmax为粒径下限，P为孔隙率，E为颗粒刚度。
表1 数值模型试样的颗粒参数
Table 1 Particle parameters of the numerical sample
2) 伺服围压机制
编写伺服程序来施加围压，具体是将边墙应力与理论围压间的差异转化为边墙位移(图3)，通过边墙的左右移动来保持围压不变[17]。假定σre为三轴试验所设定围压，σme为上一时步加压过程中2#和3#墙体受到的实际应力，则下一时步墙体水平运动速度为：
每一时步由 2#和 3#墙体运动而产生的作用力最大增量为：
式中：
为墙体法向平均接触刚度；Nc为墙体上颗粒接触数，故墙体上应力改变量为：
式中，A为 2#和 3#墙体长度。为使计算稳定，引入松弛因子α(取值范围为0～1，一般取0.5)，需满足|Δσ(w)|＜α|Δσ|，通例式(3)和式(5)即有：
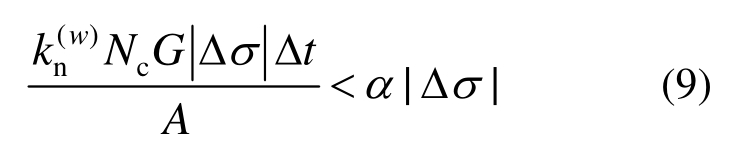
求得伺服控制参量：
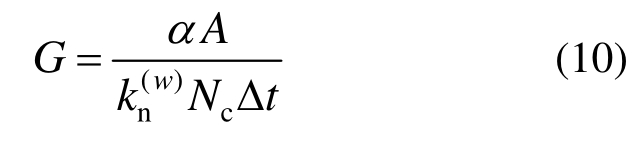
将式(10)代入式(6)便可求得侧向墙体运动速度
参考文献及结合本文试验需要将所有试验围压均设定为1 MPa。
3) 加载机制。
上下墙以相同速率的相向运动(Vp)来模拟加载，通过改变墙体运动轨迹可模拟不同加载方式，若墙体停止运动则试验结束。本文以墙体匀速运动方式模拟常规三轴压缩试验，墙体以正弦运动方式模拟三轴疲劳。
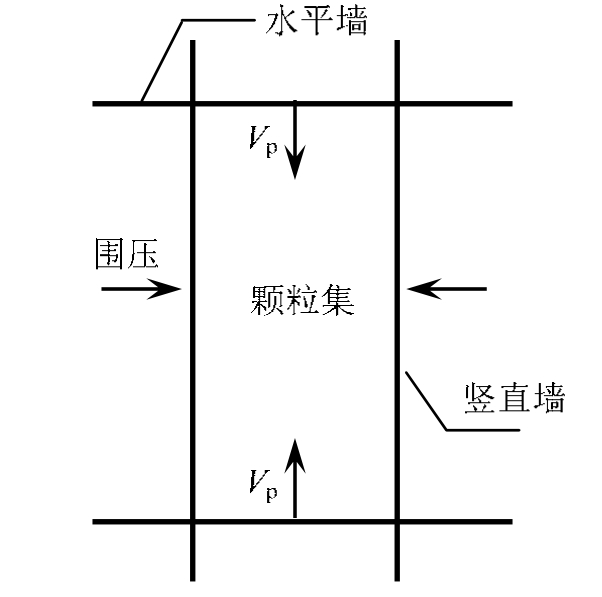
图3 PFC2D三轴模型构建
Fig.3 Triaxial model of PFC2D
1.3 细观力学参数的标定
选择黏结颗粒模型(BPM)。由于 PFC2D细观参数与实际岩石参数没有对应关系，因而细观参数不能由室内试验直接得到，为使得模拟结果具有实际意义和代表性，就需要进行细观参数的标定。PFC2D细观参数标定常以颗粒模型试样应力-应变关系与岩石试验的一致性为标准。如果在固定颗粒大小及组装方式的前提下，只改变颗粒间相互作用(本构关系)力学参数的标定过程称为细观力学参数标定。PFC2D细观力学参数标定是一个繁复过程，需要进行参数的反复尝试。
大光包滑坡是汶川地震触发的最大滑坡，其滑床岩体为震旦系灯影组白云岩，建造受控于海相沉积环境，转为陆相沉积后因构造变动发生破裂，后经热液充填形成方解石斑团，是一种典型含团状缺陷结构岩石[18]，前人对该岩体力学特性及影响因素进行过系统研究[19]。本文选择汶川地震大光包滑坡滑床白云岩进行参数标定。经过反复调整得到颗粒模型试样与所选岩样应力-应变曲线基本重合(图 4)，保证弹性模量、峰值强度、泊松比等参数差异<3%的一组细观力学参数如表2，其中f为接触摩擦系数，cσ为法向黏结强度，cτ为切向黏结强度，
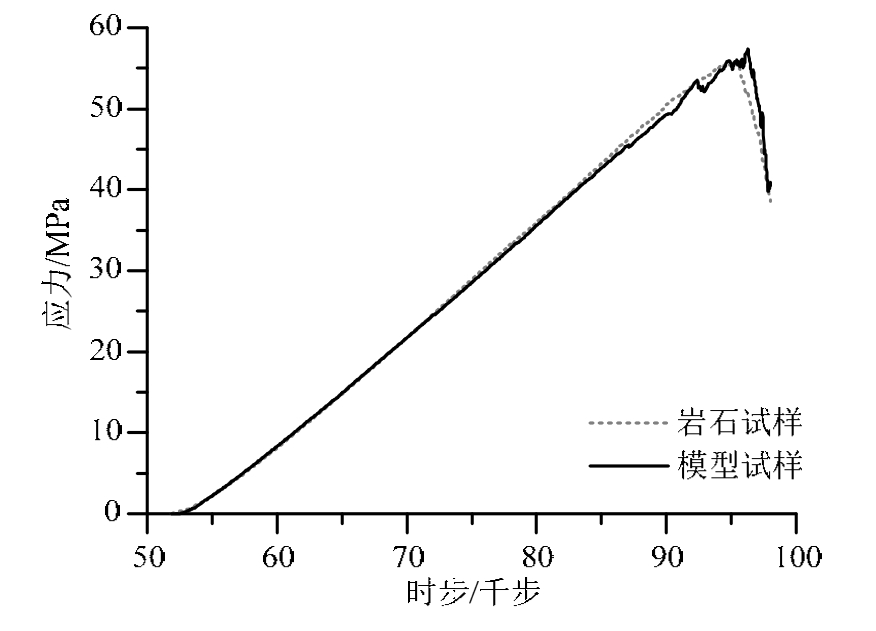
图4 细观参数标定
Fig.4 Micro-mechanical parameters calibration
表2 数值模型试样的细观力学参数
Table 2 Meso-mechanical parameters in PFC2Dmodel
注：kn为法向黏结刚度，ks为切向黏结刚度。
1.4 试验方案
本文在常规三轴试验试样尺度下，不考虑团块缺陷个数和大小等因素，分析不同软弱程度的相同大小、单一团块缺陷对岩石试样力学特性影响。将生成的颗粒试样中部半径 1 cm圆形区域设定为团块，通过改变团块颗粒黏结强度参数(
为法向黏结强度，
为切向黏结强度，
为法向黏结刚度，
为切向黏结刚度)分析团块对试样力学性质影响。选择4个细观参数，并取0.1倍、1倍和10倍设定三种团块类型，而保持其他参数不变，见表3。
表3 试验方案
Table 3 Test program
各试样分别进行普通三轴压缩试验和三轴疲劳试验。本文不考虑加载信号影响因素，对所有试样进行统一设定。疲劳试验采用正弦波模拟疲劳荷载，设定上限应力比(ku)为 0.9，下限应力比(kd)为0.4，利用静载试验获得的抗压强度(σc)计算上限应力(σmax=kd×σc)，下限应力(σmin=ku×σc)和振动幅值(Δσ=σmax-σmin)。前人对大光包滑坡白云岩进行的 MTS岩石三轴试验频率范围在 0.25 Hz～0.5 Hz[19]，本文设定加载频率为0.4 Hz。
由于PFC试样由颗粒组成，可监测单个颗粒力学行为，也可设置某一直径测量环监测环内颗粒综合力学行为。本文测量环半径为0.5 cm，分别在团块中心和边缘的上、下、左和右四个方向对称布置，分别标记为测点 4#、5#、6#、7#和 8#。4#测点能反映团块自身力学行为，其余测点则反映了团块边界力学特征。4#测点与5#、6#构成与加载方向平行的纵向监测剖面，4#与7#、8#构成了与加载方向垂直的横向监测剖面，可分析团块不同方向力学性质差异。由于加载中环内颗粒不但发生变形而且产生位移，故用应变率反映测点变形[15]。设颗粒临近两点应变dui=aijdxj，则这两点速度差为dvi=
其中
为应变率，用张量形式给出：
式中，
分别为位移张量和转动张量。测量环所测应变率张量用环内所有颗粒相对速度平均值代表：
式中，
为测量环内颗粒平均位置。生成的含团块颗粒模型试样和监测点布置如图5。
图5 三轴数值模型试样及监测点
Fig.5 Numerical sample and measure point
2 模拟结果
2.1 破坏特征
A、B和C三类试样三轴压缩试验结果如图6所示。A试样团块发生压缩变形，同时被两条剪裂面剪切破坏，破坏裂纹与加载方向夹角约 40°(图6(a))。B类试样破坏形式与A基本一致，不同的是右侧剪裂面并未贯穿试样，而于中部转折表现出张拉特征(图 6(b))。C类试样破坏形式与前两者有较大差别，表现为团块未发生明显变形和破坏，且破裂面发育在团块上方，而团块以下试样基本未破坏(图 6(c))。结果表明，试样内部团块的存在改变了试样破坏方式。
A、B和C动载试验结果如图6所示。A类试样团块发生塑性变形，但团块未被剪切破坏，而团块周围裂纹发育(图 6(d))；B类试样产生与静载几乎相同的破坏方式，但与静载相比破裂面表现出更高的碎裂程度(图 6(e))；C类试样团块未发生变形破坏，而团块上方和下方各发育剪裂面和微细裂纹(图 6(f))。
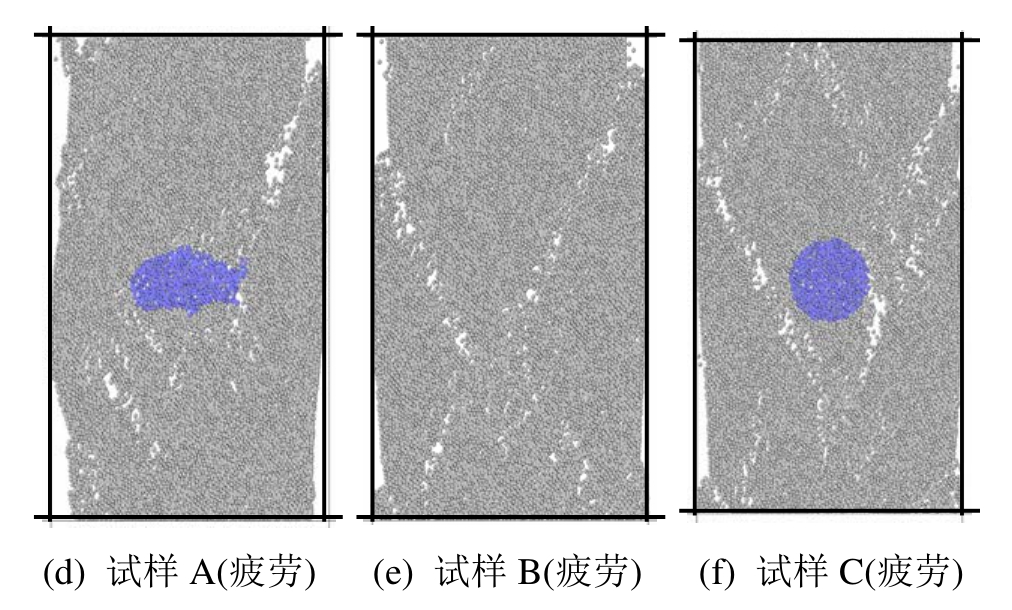
图6 试验结果
Fig.6 Test results
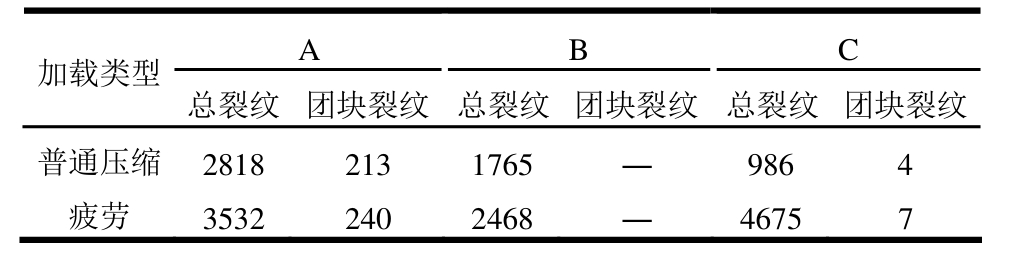
通过PFC2D子程序统计加载结束时试样微裂纹(表4)，结果显示普通压缩下A类试样发育总裂纹和团块内部裂纹多于B类和C类试样；动载下三类试样总裂纹条数均增加，尤其是A类和C类试样幅度较大；无论静载或动载，C类试样团块内部裂纹不发育。
表4 微裂纹统计
Table 4 Statistics of microcrack
2.2 应力-时步曲线
图7显示了普通压缩和疲劳下试样各监测点应力-时步曲线。A 类试样纵向监测点(4#、5#和 6#)应力随时步变化情况基本一致，前期应力随时步呈直线增加，在约80千时步时达到应力峰值(28 MPa)而后呈波动下降。横向监测点(7#和8#)应力-时步曲线变化基本相同，初期应力随时步呈直线快速增长，增长速率快于纵向测点，在约 85千时步时达到应力峰值(约50 MPa)，而后应力陡降，显脆性破坏(图7(a))。B类试样各测点应力-时步曲线变化基本相同，表现为峰前直线增长与峰后应力陡降特征，在约 94千时步达到峰值应力(55 MPa～60 MPa)(图7(b))。与A类试样不同，C类试样纵向4#、5#和6#测点应力-时步曲线位于7#和8#之上，峰前各测点曲线变化基本相同，在约 97千时步达到峰值应力(46 MPa～55 MPa)，其中 6#测点应力最大，7#测点最小，而后应力突然降低(图 7(c))。上述结果表明试样内部应力差异分布。
动载下试样各测点的应力变化特征与静载基本相同(如图7)，当团块颗粒强度低于试样时，4#、5#和6#测点动应力低于7#和8#测点(图7(d))，而当团块颗粒强度高于试样时，前者应力高于后者(图7(e))，当无团块结构时5个测点应力-时步曲线基本重合(图7(f))。对于A类、C类试样，各测点振动起始应力不相同，这是各测点处应力分布不均导致的，这一点从压缩试验可以看出。
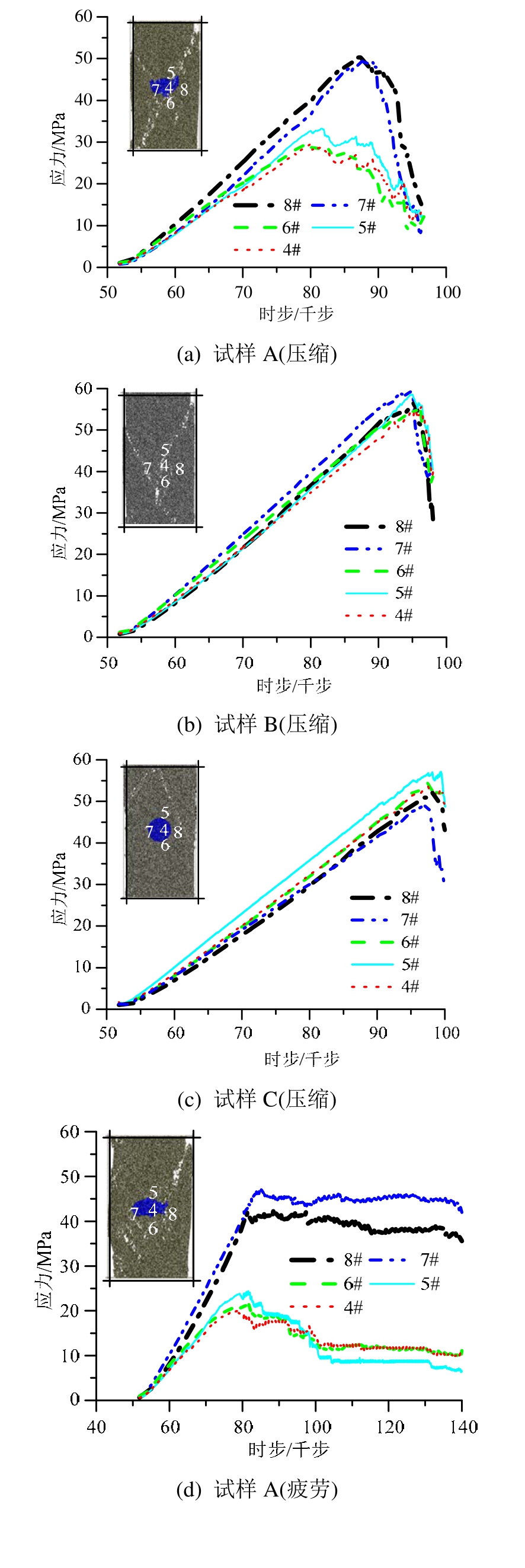
图7 应力-时步曲线
Fig.7 Stress-time step curves
2.3 应变率-时步曲线
取压缩试验4#、5#和7#三测点相同时步区间进行应变率分析(图8)，可以看出同一试样三轴压缩试验中三测点应变率存在差异，具体表现为A类试样4#测点应变率大于其余两测点(图8(a))，B类试样三测点应变率大小基本相等且变化基本同步(图8(b))，C类试样4#测点应变率小于其余两测点(图8(c))。
疲劳试验的应变率-时步曲线呈现出更丰富特征(图9)。A类试样4#测点应变率上限约0.7，幅值约为1.5，其值大于其余4个测点(图9(a))；C类试样4#测点应变率上限约0.25，幅值约0.6，其值小于其余测点(图9(c))；而B类试样各测点应变率大小和变化步调基本一致，应变率上限约0.5，幅值约1(图9(b))。对于A类、C类试样，(纵向上)4#测点应变率变化波形与5#、6#测点形成错位，而与(横向上)7#、8#测点却几乎一致。
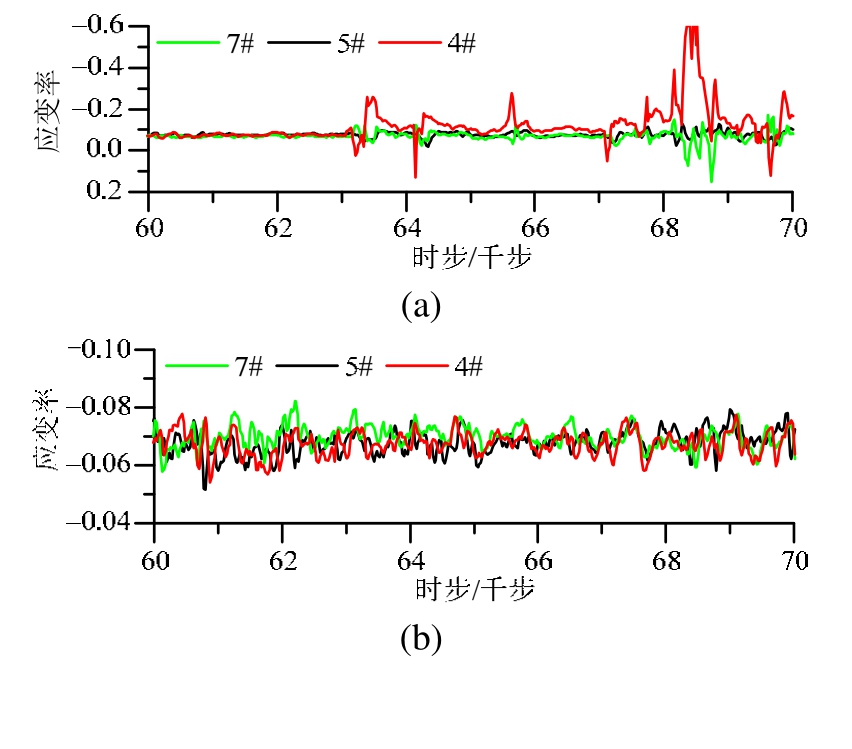
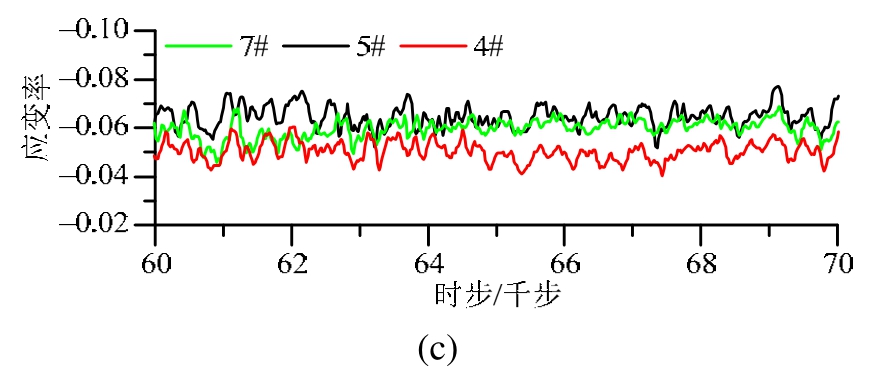
图8 应变率-時步曲线(压缩)
Fig.8 Strain ratio-time step curves (Comp.)
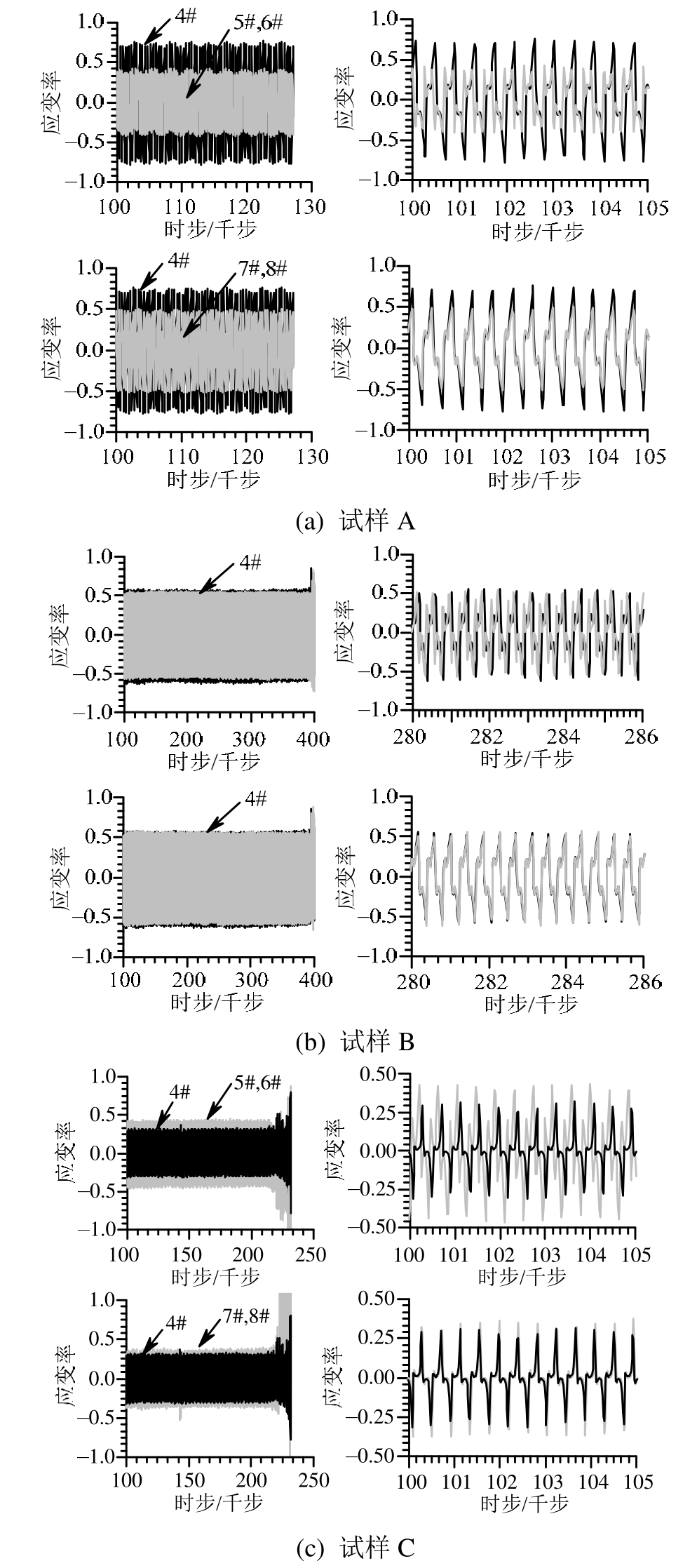
图9 应变率过程曲线(疲劳)
Fig.9 Strain ratio-time step curves (Cyclic)
3 力学特性影响分析
3.1 强度劣化
三类试样应力-应变曲线如图10所示，可以看出 A类试样弹性模量最低(表现为峰前曲线直线段斜率最小)，峰值强度最小，约42 MPa；虽然C类试样团块细观力学参数大于B试样，但其弹性模量和峰值强度(约 51 MPa)仍小于 B类试样(约58 MPa)。结果表明，虽然三类试样除团块外颗粒细观参数完全相同，但团块无论强度高低均影响试样应力-应变过程，而且劣化试样整体强度。
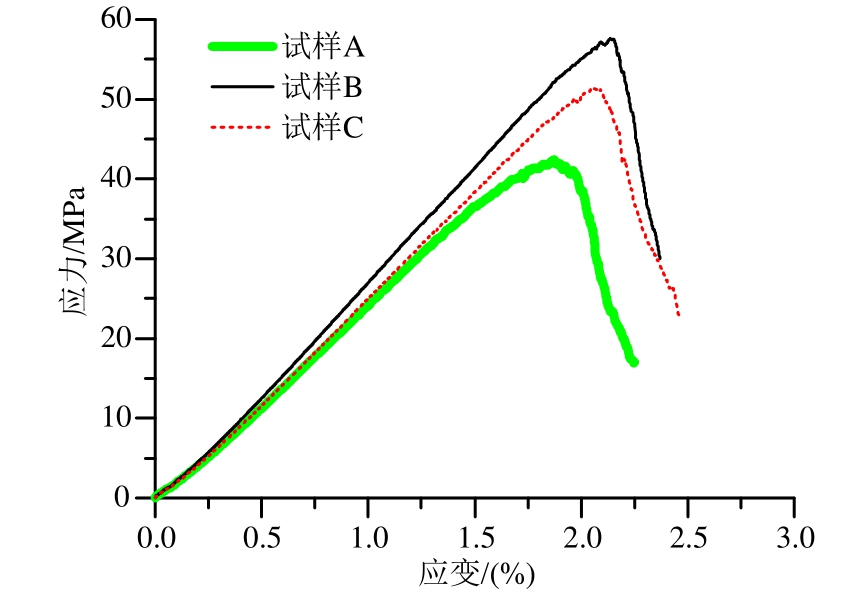
图10 应力-应变曲线
Fig.10 Stress-strain curves
3.2 应力集中
将各试样总应力-时步曲线与 4#测点应力-时步曲线进行对比(图11)，可以看出除C类试样外其余试样两曲线均呈现较大差异，表现为A类试样团块中心应力小于试样宏观应力(整体应力)(图11(a))，而C类试样团块中心应力大于试样宏观应力(图11(c))，结合图7(a)～图7(c)，表明含团块试样的整体应力与局部应力不一致，即试样内部应力差异分布。值得注意的是该应力差异在试样弹性变形阶段已经出现(图11)，而并非是试样发生破坏时才开始的。
比较A、B和C类试样中心(4#)应力峰值大小(图11(d))，A类试样4#应力峰值最小，这是由于A类试样团块强度最低，当应力超过其强度时便首先产生破坏，而此应力水平对于其余测点位置还处于弹性(或弹塑性)阶段(图7(a))；B类试样和C类试样中心应力峰值基本相同(图 7(b)、图 7(c))，这是由于C类试样团块强度高，当团块外部发生破坏的应力水平并未超过团块强度阀值，所以其峰值应力反应的是其块外部颗粒黏结强度的破坏。
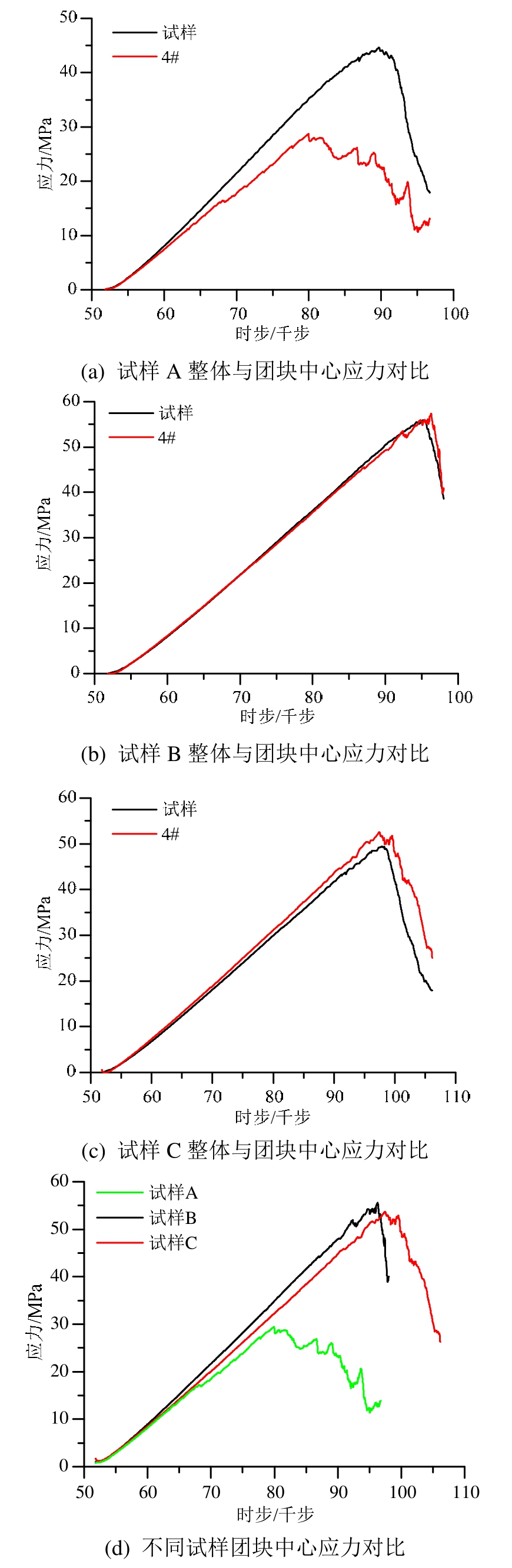
图11 团块对试样应力分布影响
Fig.11 Influence of block mass on stress
结合应力测量结果可以推测，若团块颗粒强度低于试样，则应力集中在与加载方向垂直的团块左右两侧(图12(a))；若团块颗粒强度高于试样强度，则应力集中在与加载方向一致的团块上下两侧(图12(b))。以上分析表明含团块试样破坏是从应力差异分布导致的局部破坏开始的。
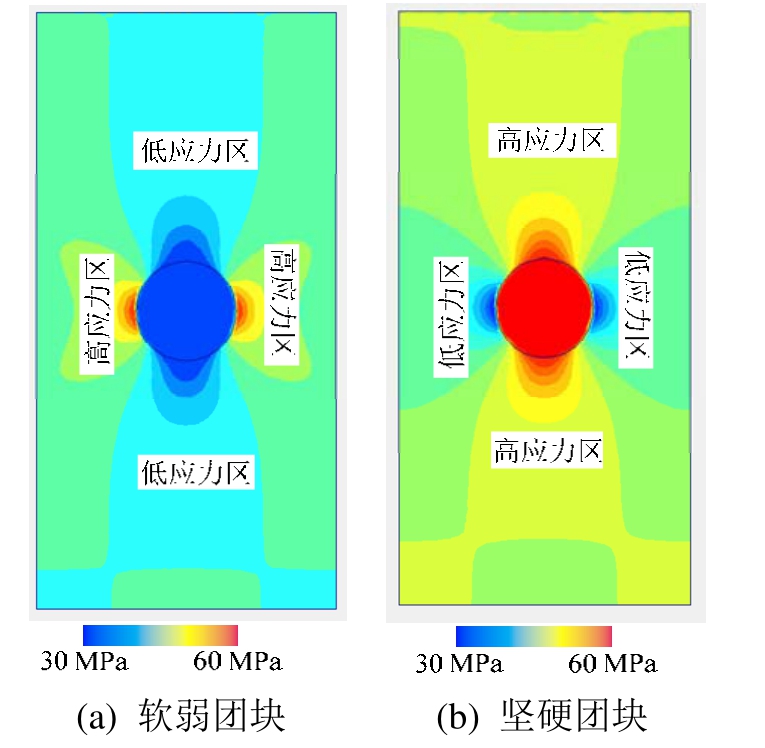
图12 含团块试验加载的应力分布
Fig.12 Stress distribution in sample with block mass
3.3 差异性变形
由疲劳试样应变率-时步曲线(图 9)分析可知，在相同加载条件下，低强度团块应变率大于周围，反之变小，由此表明含团块试样内部应变率分布同样具有差异性。对三类试样各测点应变率对比分析(图13)，结果表明，A类试样大于B类试样，C类试样小于B类试样。值得注意的是破坏时C类试样应变率均骤然增大，是由于试样破坏造成的团块卸荷回弹，由于A类试样团块强度最低，所以回弹变形最小。三类试样各测点应变率相对大小规律虽然相同，但差异明显减小。位于中心的4#测点差异最大，而向两测(5#、6#和7#、8#)差异变小；其中在与加载方向平行的纵向(5#、6#)差异又大于与加载方向垂直的横向(7#、8#)。虽然未在更远离团块位置设置测点，但可以推测随着与团块距离增大应变率差异应更小或甚至为零。
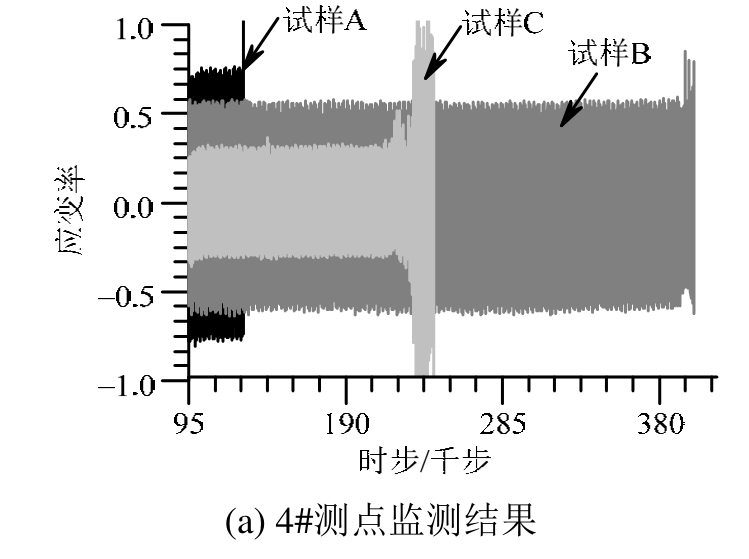
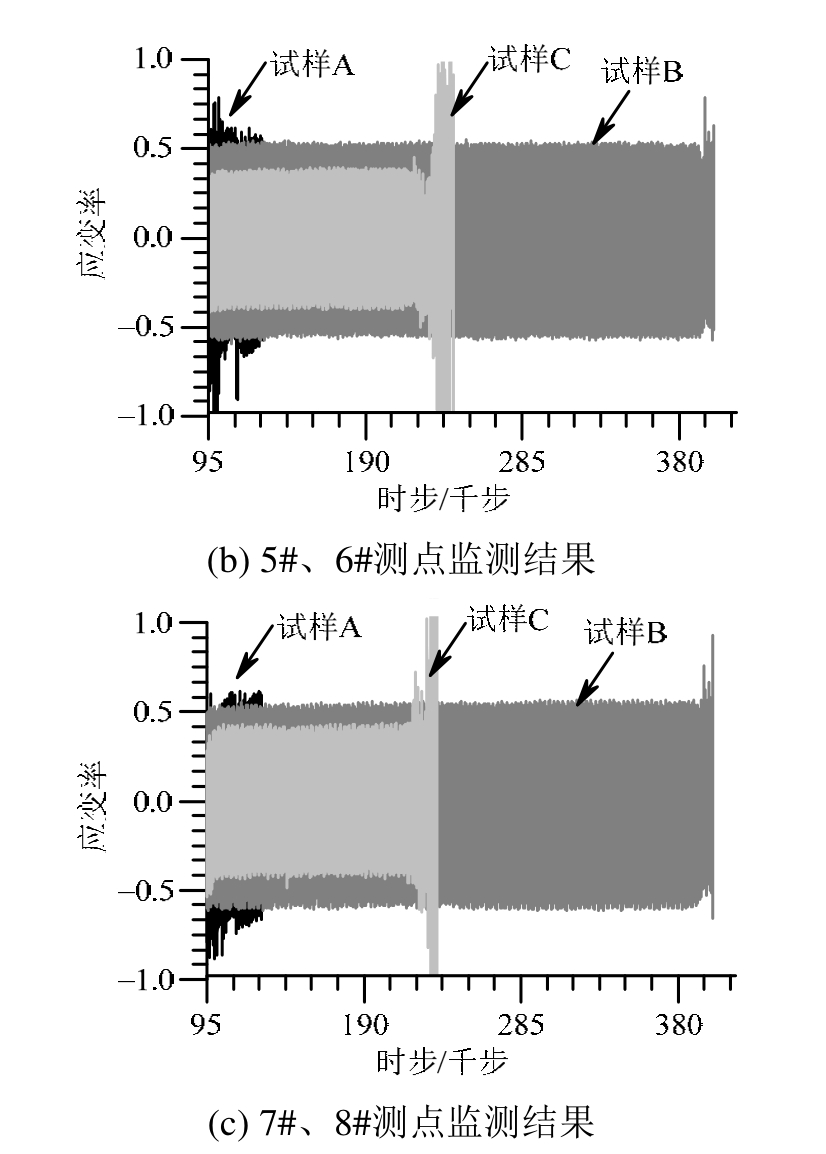
图13 团块对应变率分布影响
Fig.13 Influence of block mass on strain ratio
由应变率-时步曲线结果可知，压缩过程中含团块缺陷岩石应变表现出分异特征，若团块材料强度低于试样，则团块内部应变率高于外部，反之团块内部应变率低于外部。疲劳荷载下不但存在应变率大小不同，而且在与加载方向垂直方向上，团块中心与两侧不但存在大小差异，而且波型(步调)也不一致。
4 讨论与结论
在经典弹塑性力学中有一个重要假定，即材料的连续性假定，也即是说介质无空隙地分布于物体所占的整个空间，其发生变形为协调变形。假想将一个连续材料分割为若干单元，对材料整体施加外力后，材料将发生弹塑性变形，每一个单元也将产生各自变形；协调变形理论指出，在变形过程中这些单元之间不产生开裂，即将这些变形单元拆开后能无缝地重新拼合，从数学上表述为变形产生的位移函数是定义域内的单值连续函数[20]。若材料性质不连续，如含缺陷结构，那么材料变形将不协调，在结构部分产生变形突变，导致拉、剪应力，使完整材料强度和模量发生显著劣化[21－23]。本文研究表明，含团块试样由于团块与试样强度差异导致了试样内部应力的差异分布，造成局部应力集中或低应力区。宏观上对试样施加相同应力，若试样内部单元均发生弹性连续变形，则应力将在试样内部均匀分布；若部分单元发生弹性变形，而另一部分发生塑性变形，或弹性(塑性)变形大小不同，则变形差异必然使得大变形区应力低，小变形区应力集中，从而形成不均匀应力场。在疲劳过程中，试样形变是周期发生的，一方面前述应变差异引起的应力集中可能造成试样局部压剪破坏；另一方面，加载时不同单元弹塑性变形不同，可能造成卸荷差异回弹，从而在单元间形成拉张应力，由于岩体抗拉强度低，该拉应力可能形成局部拉破坏(图14)。局部拉张、压剪破坏的逐渐聚集和扩展导致试样整体强度劣化。该机理也使得疲劳荷载下试样碎裂程度大于压缩荷载。
通过研究，本文得到以下结论：
(1) 岩石内部团块状结构无论强度高低均劣化岩石强度。
(2) 加载过程中，含团块结构岩石内部应力场表现出不均匀性。具体表现为，若团块材料强度低于试样强度则与加载方向垂直的团块两侧应力集中，而与加载方向平行的团块两侧，包括团块内部为低应力区；若团块材料强度高于试样材料强度，则与加载方向垂直位置为低应力区，而与加载方向平行位置，包括团块内部为应力集中。
(3) 加载过程中，含团块结构岩石非协调变形。具体表现为，若团块材料强度低于试样强度，则团块内部应变率高于外部，反之团块内部应变率低于外部。
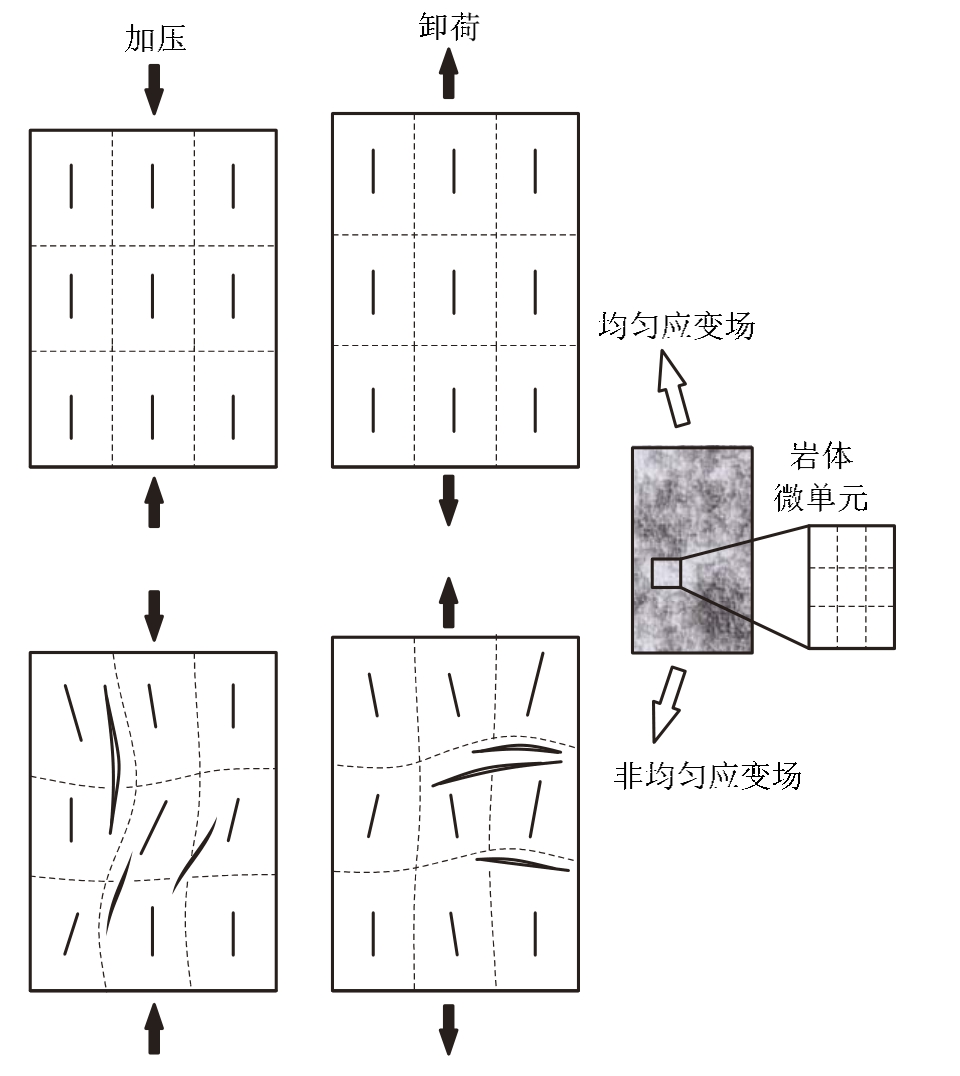
图14 岩体协调与非协调变形
Fig.14 Compatible and non-compatible deformation
参考文献：
[1]Jing L. A review of techniques, advances and outstanding issues in numerical modeling for rock mechanics and rock engineering [J]. International Journal of Rock Mechanics and Mining Sciences, 2003, 40(3):283―353.
[2]Hudson J A, Harrison J. Engineering rock mechanics：an introduction to the principles [M]. Oxford: Elsevier Cience Ltd., 1997: 23.
[3]Dey T N, Wang C Y. Some mechanisms of microcrack growth and interaction in compressive rock failure [J].International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, 1981, 18(3):199―209.
[4]苏海健, 靖洪文, 赵洪辉, 等. 平行裂隙群岩体强度与破裂特征的试验研究[J]. 工程力学, 2015, 32(5): 192―197.Su Haijian, Jian Hongwen, Zhao Honghui, et al. Strength and fracture characteristic of rock mass containing parallel fissures [J]. Engineering Mechanics, 2015, 32(5):192―197. (in Chinese)
[5]Bobet A. Modelling of crack initiation, propagation and coalescence in uniaxial compression [J]. Rock Mechanics and Rock Engineering, 2000, 33(2): 119―139.
[6]Szwedzicki T. A hypothesis on modes of failure of rock samples tested in uniaxial compression [J]. Rock Mechanics and Rock Engineering, 2007, 40(1): 97―104.
[7]Jeong H S, Kang S S, Obara Y. Influence of surrounding environments and strain rates on the strength of rock subjected to uniaxial compression [J]. International Journal of Rock Mechanics and Mining Sciences, 2007,44(3): 321―331.
[8]邸元, 康志江, 代亚非, 等. 复杂多孔介质多重介质模型的表征单元体[J]. 工程力学, 2015, 32(12): 33―39.Di Yuan, Kang Zhijiang, Dai Yafei, et al. Representative elementary volume of the multiple-continuum model for complex porous media [J]. Engineering Mechanics,2015, 32(12): 33―39. (in Chinese)
[9]朱合华, 黄伯麒, 张琦, 等. 基于广义 Hoek-Brown准则的弹塑性本构模型及其数值实现[J]. 工程力学,2016, 33(2): 41―49.Zhu Hehua, Huang Boqi, Zhang Qi, et al. Elastoplastic rock constitutive model based on generalized Hoek-brown strength criterion and its numerical implementation [J]. Engineering Mechanics, 2016, 33(2):41―49. (in Chinese)
[10]Wang S H, Lee C I, Ranjith P G, et al. Modeling the effects of heterogeneity and anisotropy on the excavation damaged/disturbed zone (EDZ) [J]. Rock Mechanics and Rock Engineering, 2009, 42(2): 229―258.
[11]刘招伟, 李元海. 含孔洞岩石单轴压缩下变形破裂规律的实验研究[J]. 工程力学, 2010, 27(8): 133―139.Liu Zhaowei, Li Yuanhai. Experimental investigation on the deformation and crack behavior of rock specimen with a hole undergoing uniaxial compressive load [J].Engineering Mechanics, 2010, 27(8): 133―139. (in Chinese)
[12]Rodionov V N, Sizov I A. Appearance of nonuniformity of the stressed state as a result of fracture of rocks [J].Journal of Mining Science, 1982, 18(6): 323―331.
[13]刘晓丽, 王思敬, 王恩志, 等. 单轴压缩岩石中缺陷的演化规律及岩石强度[J]. 岩石力学与工程学报, 2008,27(6): 1195―1201.Liu Xiaoli, Wang Sijing, Wang Enzhi, et al. Eeolutionary rules of flaws in rock subjected to uniaxial compression and rock strength [J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(6): 1195―1201.(in Chinese)
[14]Cundall P A, Strack O D L. A discrete numerical model for granular assemblies [J]. Geotechnique, 1979, 29(1):47―65.
[15]Itasca Consulting Group. PFC2D (Particle flow code in 2 dimensions) user′s guide [R]. Minneapolis, USA: Itasca Consulting Group, 2008: 44―45.
[16]周维垣. 高等岩石力学[M]. 北京: 水利电力出版社,1990: 216―243.Zhou Weiyuan. Advanced rock mechanics [M]. Beijing:Water Resources and Electric Power Press, 1990: 216―243. (in Chinese)
[17]Itasca Consulting Group. PFC2D (particle flow code in 2 dimensions) fish in PFC2D [R]. Minneapolis, USA:Itasca Consulting Group, 2008: 20―22.
[18]崔圣华. 强震巨型滑坡滑带碎裂岩体微细观分析及静动力破损机制研究——以安县大光包滑坡为例[D].成都: 成都理工大学, 2014.Cui Shenghua. Microstructure and static dynamics damage mechanism of the slipping cataclastic rock of the largest scale landslide - a case of Daguangbao landslide in Anxian [D]. Chengdu: Chengdu University of Technology, 2014. (in Chinese)
[19]罗璟, 裴向军, 黄润秋, 等. 强震作用下滑坡岩体震裂损伤程度影响因素研究[J]. 岩土工程学报, 2015,37(6): 1105―1114.Luo Jing, Pei Xiangjun, Huang Runqiu, et al. Influencing factors of the damage degree of seismic shattered landslide rock mass under highly seismic action [J].Chinese Journal of Geotechnical Engineering, 2015,37(6): 1105―1114. (in Chinese)
[20]陈宗基, 康文法. 在岩石破坏和地震之前与时间有关的扩容[J]. 岩石力学与工程学报, 1983, 2(1): 11―21.Chen Zongji, Kang Wenfa. Time dependent dilatancy prior to rock failure and earthquakes [J]. Chinese Journal of Rock Mechanism an Engineering, 1983, 2(1): 11―21.(in Chinese)
[21]杜明瑞, 靖洪文, 苏海健, 等. 孔洞形状对砂岩强度及破坏特征的影响[J]. 工程力学, 2016, 33(7): 190―196.Du Mingrui, Jing Hongwen, Shu Haijian, et al. Effects of holes’ geometrical shape on strength and failure characteristics of a sandstone sample containing a single hole [J]. Engineering Mechanics, 2016, 33(7): 190―196.(in Chinese)
[22]Janeiro R P, Einstein H H. Experimental study of the cracking behavior of specimens containing inclusions(under uniaxial compression) [J]. International Journal of Fracture, 2010, 164(1): 83―102.
[23]Pan P Z, Feng X T, Hudson J A. The influence of the intermediate principal stress on rock failure behaviour: A numerical study [J]. Engineering Geology, 2012, 124(1):109―118.