弱形式求积元[1](Weak-form Quadrature Element)是一类基于微分方程的弱形式描述离散和求解数学及工程问题的方法。它的主要思想方法来源于Bellman和Casti[2]于1971年提出的微分求积法(Differential Quadrature Method)，并结合了高效的数值积分工具，将单元内未知的连续函数信息完全离散在一套精心选择的格点上。通过对这样一套格点上函数值的线性组合，未知函数在各格点处的导数值及其在整个单元内的积分值都能够较为精确地获得。求解的过程完全分解成一系列矩阵运算。由于数值积分点和微分求积点始终保持一致，既免去了重新插值的过程，又简化了数据的存储。这种运算的简化在处理非均匀介质[3]，带界面滑移的组合结构[4]，以及结构非线性变形[5]，动力响应分析[6]等方面已经充分得到展示。
三角形求积元是弱形式求积元中必不可少的一种二维单元，对于处理复杂几何区域问题有着不可替代的作用。基于微分求积点和积分点一致的原则，将基于等间距格点的三角形微分求积法[7](Triangular Differential Quadrature Method)直接拓展到弱形式求解面临着微分和积分均存在大幅的正负相消的问题。尽管可以通过将微分求积局域化[8]和降阶积分的方法减轻这两种不稳定性，但随之而来的单元阶数的损失却大大降低了求解的精度和效率。较为合理的改进措施是采用非均匀格点。一方面将格点向边角处集中能够有效降低插值函数的振荡，另一方面积分权系数能够全为正或只产生少量绝对值很小的负值。本文作者近期提出的从球面三角形映射产生的非均匀格点[9―10]就是这样的一种尝试。格点的产生类比于一维Chebyshev点[11]的产生方式，在保证总点数和各层点数不变的前提下，利用球面自身的曲率将球面三角形上分布较为均匀的格点通过平方其面积坐标的方式映射为平面三角形上边角处较为集中的格点。数值实验表明这样的非均匀格点单元收敛速度较均匀格点单元有显著的提升。
本文尝试对上述单元进一步改进，主要着眼点是积分的精度。在弱形式求解中，数值积分通常要完成对未知函数或者其导数的内积，理想的状况是用于近似的多项式函数精确积分的阶数能够接近插值多项式阶数的2倍，对于椭圆型二阶偏微分方程，积分阶数至少需要达到2n-2[12]。目前文献中还没有满足这样条件的插值型积分，文献[13]证明了积分阶数为2n-1的法则是不存在的。因此本文放松对积分精度的要求，在保证格点分布具有等边三角形完全对称性的前提下，利用格点位置和积分权系数的自由度，尽可能使更多的多项式得以精确积分，最终得到了积分阶数大约为插值阶数1.6倍的数值积分法则。积分的权系数均为正。将构造的单元应用于平面位势和平面弹性问题的求解，比较了优化前后的收敛情况。数值算例表明积分精度的改善对单元升阶过程中的稳定性有重要的影响。
1 球面映射点和积分的优化
通过球面映射方式产生非均匀格点的方式和公式推导在文献[9―10]中有详细的介绍，这里做简单回顾。在一个三维正交坐标系中选取单位球面x2+y2+z2=1在第一象限的部分(一个球面三角形)，对于给定的单元阶数n，寻找这样的点集(x,y,z)使得连接它和三个顶点(1,0,0)(0,1,0)(0,0,1)的大圆弧将球面三角形分成三个小的球面三角形，其面积与总面积的比值分别为(p/n,q/n,r/n)，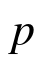
、q、r为非负整数且满足
通过球面几何中立体角和坐标的关系可推导出三个坐标的显示表达式[9―10,14]：
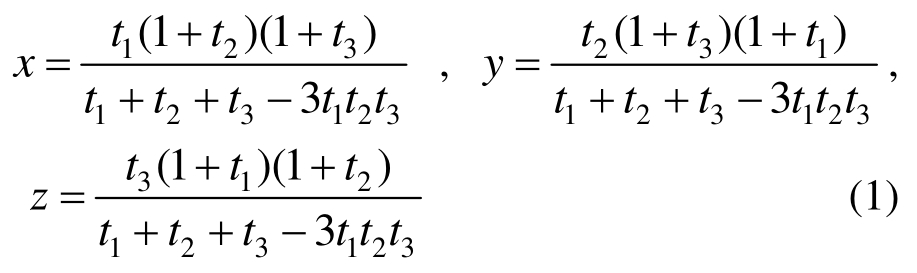
其中：
平面三角形内格点的面积坐标(ξ,η,ζ)则由下面的映射得到：
优化积分是调整积分点位置和权系数以期更高阶多项式能够被精确积分的过程。三角形内小于等于d阶的多项式空间为span{ξiηj,i+j≤d}，精确积分需要满足下面的非线性方程组：
其中：0≤i,j,i+j≤d；wk是积分点(ξk,ηk)的权系数； np=(n+1)(n+2)/2是总点数。随着阶数的增加，这一系统会呈现病态的趋势。采用三角形内的正交多项式[15―16]可以避免条件数的急剧增加。以球面映射点为初值，且假设在优化过程中每个点的对称性保持不变，可以计算出系统总的自由度数目为：
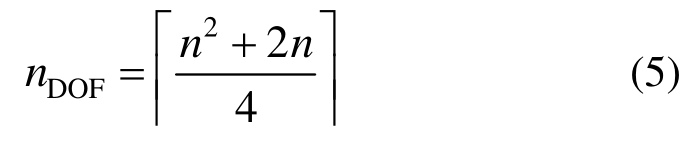
式中，括号表示向上取整。同时考虑对称性后所需要满足的多项式的数目为[17]：
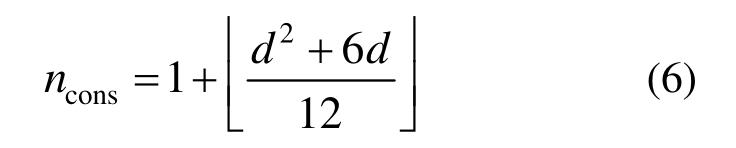
式中，括号表示向下取整。注意到式(4)实际上是一个非线性方程组，解的存在性还不存在严格的数学证明。如果按照线性方程组存在解的条件ncons≤nDOF可以求得对于每一个n、d所能取的最大值。文献中报道的三角形内数值积分法则也基本受这一条件控制[17]。通过二次项系数的比较，粗略估计
数值优化方法将式(4)看作一个非线性最小二乘问题，目标是最终误差的模小于机器精度|ε|≤10-16，可采用的优化方法有 LMA[18](Levenberg-Marquardt algorithm)，信任域(trust region)法等。首先寻找满足ncons≤nDOF最大的d值，若算法无法终止则降低d重新求解。计算的结果表明，在n＜17时积分阶数能够达到dmax-1，而17≤n≤23则能达到dmax-2。图1展示了8阶和12阶时初值和优化结果，格点的分布趋势没有改变，但积分的阶数有显著的提高。如果将各阶的积分阶数放在一起统计，平均而言优化的能够达到d≈1.6n，与确保稳定性的要求d=2n-2还有不小的差距。
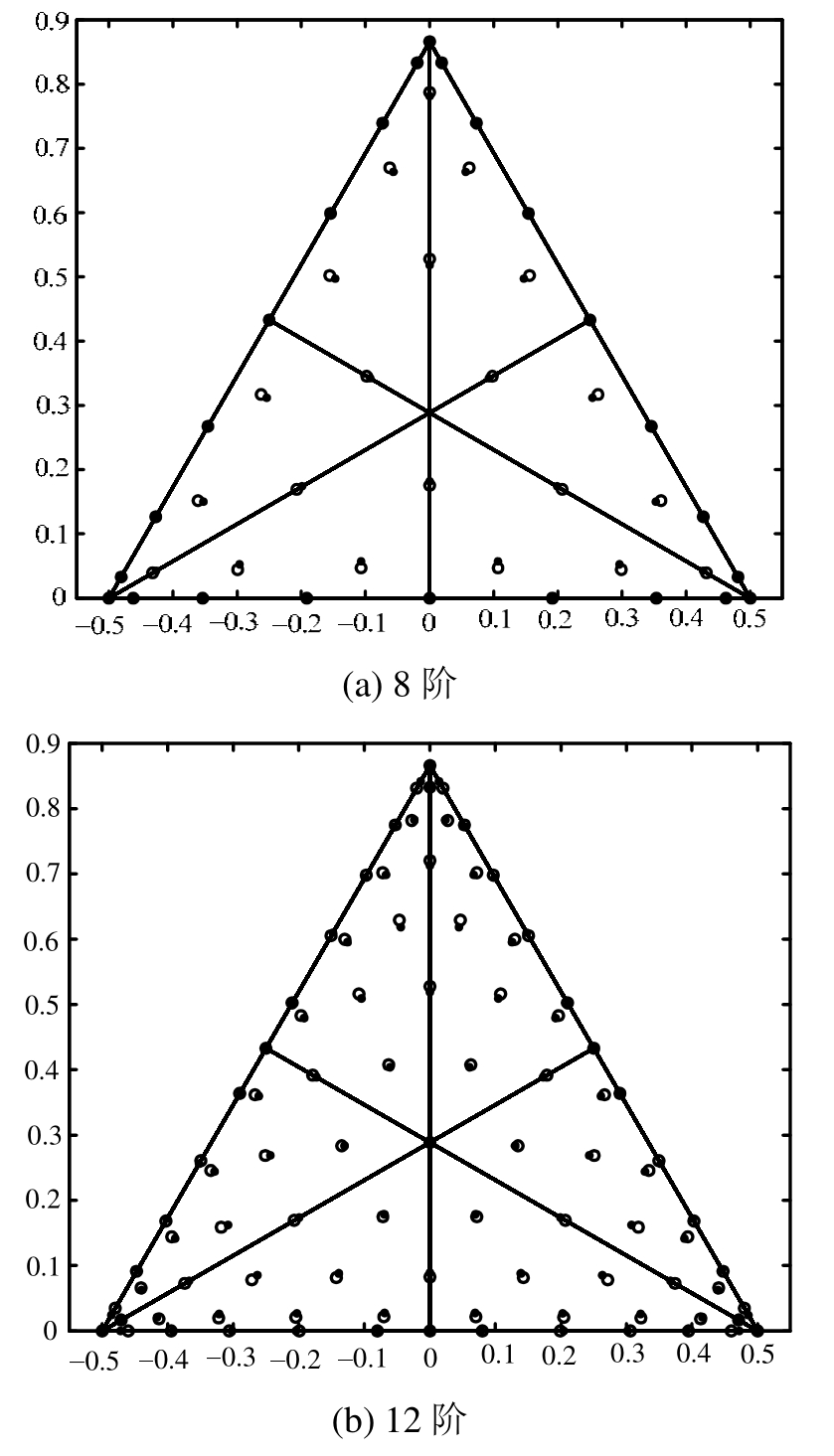
图1 8阶和12阶球面映射点(o)和优化后的积分点()
Fig.1 Spherical mapping grid and optimized grid of degrees 8 and 12
2 三角形求积元的构造
除了上面得到的数值积分外，利用多项式匹配的方法还可以在同一套点集求取一阶导数的微分求积系数：
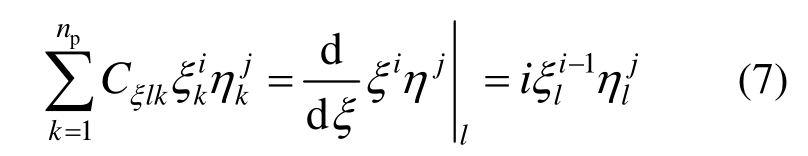
其中Cξlk表示k点的函数值对l点处ξ方向的导数的贡献。当总点数与多项式的数目一致时，它实际上是在k点处为1，其他点处为0的Lagrange插值多项式在l点处ξ方向的导数。若Lagrange多项式可以用解析表达式显式给出，则直接对其表达式求导即可，例如等间距格点的三角形微分求积法[7]；大部分情况下是无法用解析表达式显式给出的，只能通过在多项式基函数{ξiηj,i+j≤np}上对所有插值点赋值的范德蒙(Vandermonde)矩阵求逆得到。高阶导数的微分求积系数矩阵可以通过一阶的乘积得到。与数值积分的情形类似，选取式(7)中的多项式求解会造成条件数迅速增加，正交多项式是更好的选择。从基函数的正交性角度看，微分求积和积分的稳定性是由点集的正交性决定的，而正交化的过程恰恰是格点的位置的优化，分布在边角密集而中心稀疏的非均匀格点集比等间距的点集正交性更好。
得到微分求积矩阵和积分权系数后，对于不随时间变化的泛函：
通过划分求积元网格离散，可以写成所有格点上未知函数值的线性和：
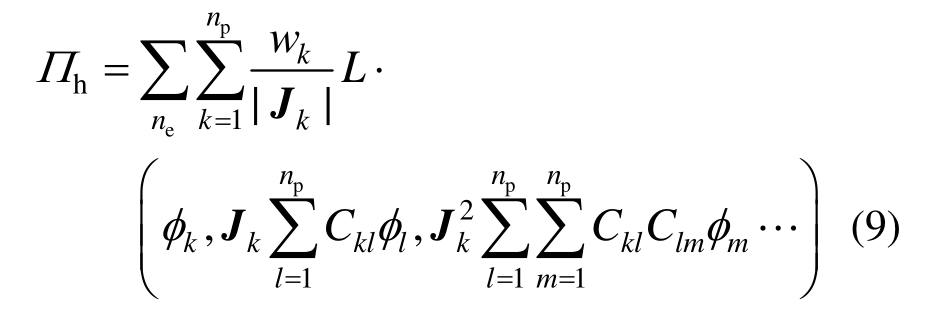
泛函取极值要求对每个点处的函数值的变分为0：从而得到关于kφ的线性方程组。
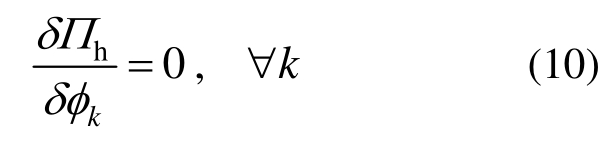
式(9)中的Jk是格点k处的2×2的 Jacobian矩阵，完成单元局部坐标系(ξ,)η和整体坐标系(x,y)之间的转换，对于直边三角形 123(角点逆时针编号)，单元上各点相同：
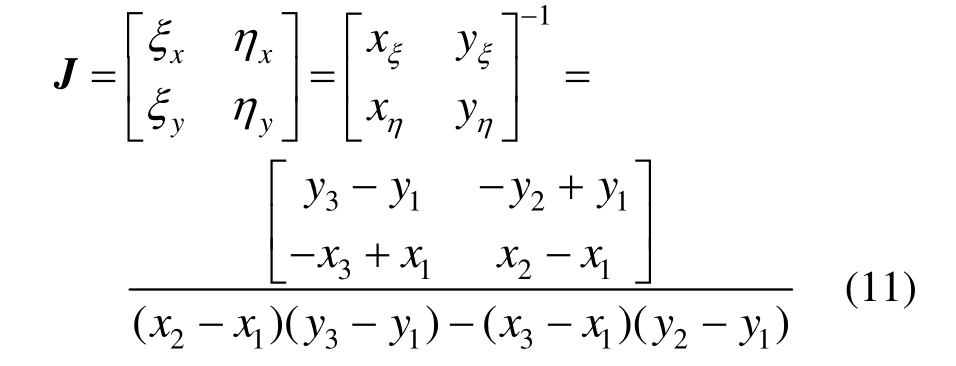
曲边三角形Jk在每个单元的每个点处都不同，它可以通过插值和微分求积获得；但对于常见的具有解析表达式曲线，更简单的是混合函数法；例如23为曲边，在曲边与相应弦边之间使用极坐标系角度θ作参数插值，一般化的表达式为：
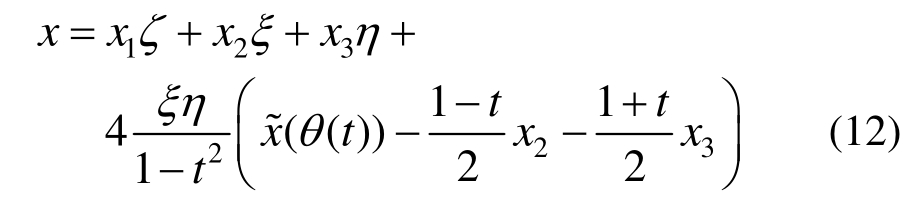
其中，-1≤t=ξ-η≤ 1。y的表达式同理可得，这里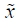
(θ)是曲边的参数化表达，θ(t)=θ2(1-t )/2+θ3(1+t)/2。将式(12)代入式(11)的前半部分并利用局域有限差分求导便可得到该点处的Jacobian。
3 算例
3.1 库克板
这是一个用来检验网格畸变对收敛性影响的平面线弹性算例，几何尺寸和材料参数如图2(a)所示，所有参数已去量纲化，边界条件为左边固支，右边受合力为1的均布向上剪力。沿较长对角线划分为两个三角形单元，求解下边A点和上边B点处的最大应力。结果均与四边形求积元收敛的结果[19](σA)max=0.2369、(σB)min=-0.2035对比。从图 2(b)和图 2(c)表明优化积分后收敛的情况有明显的改善，但是不稳定的现象并没有完全消除。
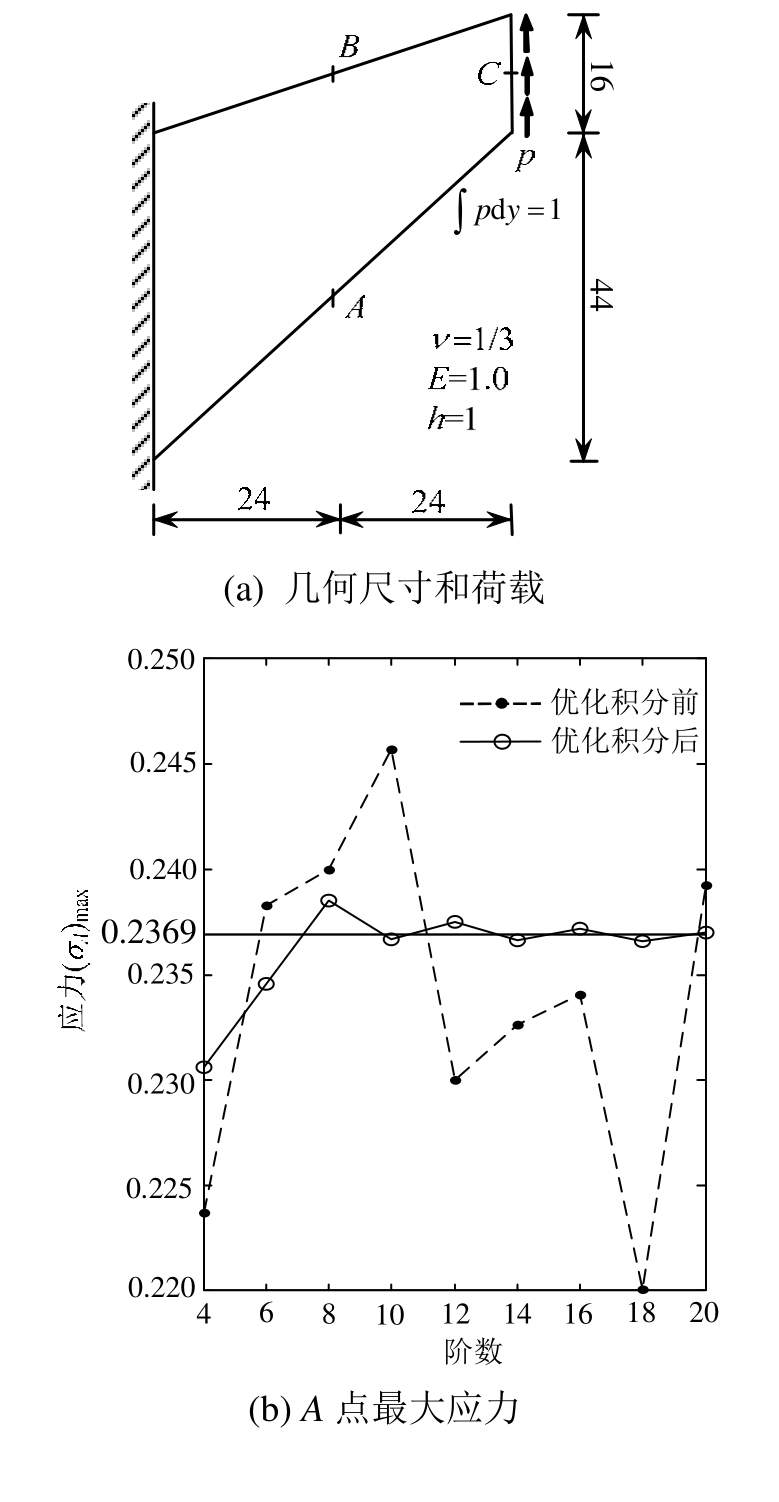
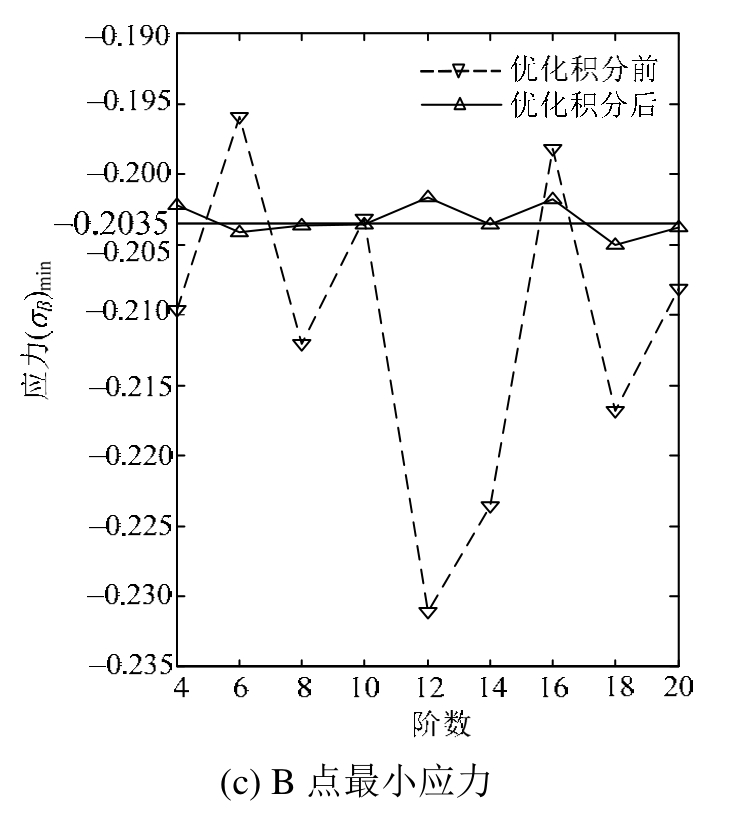
图2 库克板和计算结果
Fig.2 Cook panel and computational results
3.2 刻槽等直圆柱杆扭转
图3(a)显示了一个左侧边缘处刻有半径为b圆槽的圆柱形等直杆的横截面，杆半径为 a。槽的圆心在大圆的边界上。整个截面受大小为2的扭转面力，对应的应力函数为 。若取上半部分ABC，则求解的偏微分方程和边界条件为：
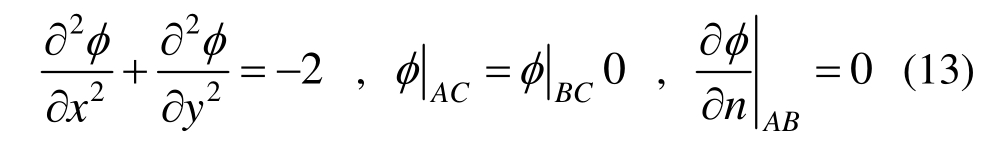
解析解为：
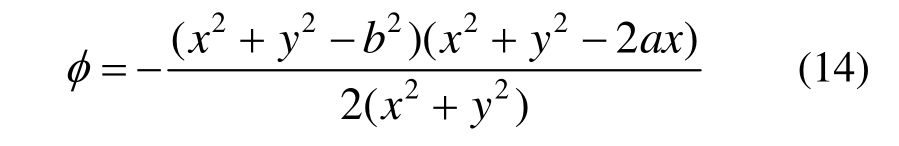
A、B两点的切向应力为：
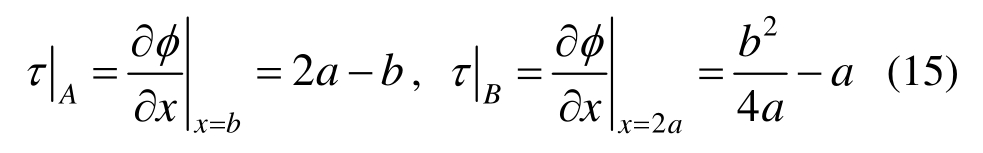
将计算域 ABC划分为四个三角形单元，如图 3(b)所示。图3(c)和图3(d)对比了a=1、b=0.3时优化前后误差减小的情况。结果表明，积分阶数的增加能明显提高计算的精度，但无法完全消除震荡。
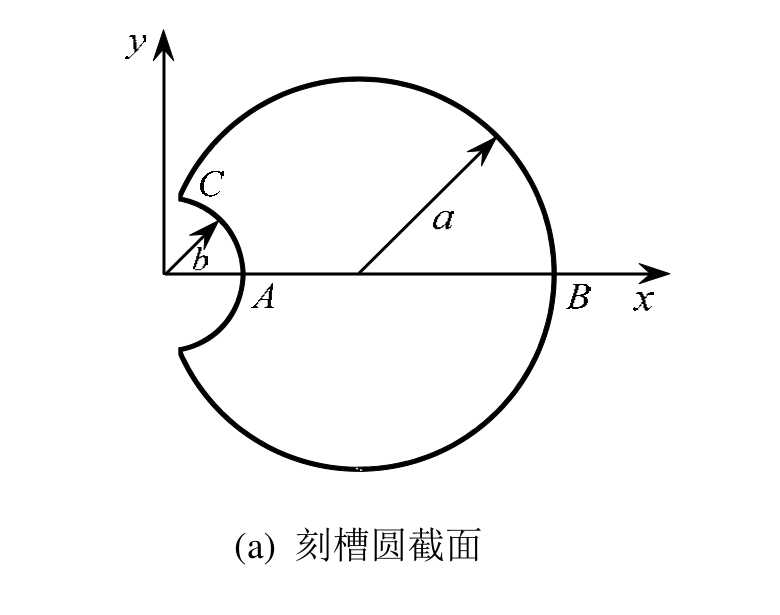
图3 刻槽圆柱杆和计算结果
Fig.3 Grooved circular shaft and computational results
4 结论与展望
本文通过优化三角形求积元非均匀格点的位置，提高了积分的阶数，从而改善了求解线性二阶偏微分方程的精度。数值实验表明积分的精度确实对于三角形求积元弱形式求解效果有重要影响。由于目前积分的阶数仍然不足插值阶数的2倍，在单元阶数升高的过程中仍然存在一定的不稳定性。进一步消除不稳定性是下一步工作的方向。本文的方法已经接近了式(5)和式(6)所决定的上限，而这个上限很可能是无法突破的。此外采用随机分布的初值可以进一步释放自由度，但是仍然十分有限，由于具有六元对称性(即不落在中线上)的点数量级上占多数，每6个点可提供3个自由度，(n+1)(n+2)/2个点能提供约n2/4个自由度，而多项式的约束个数约为d2/12，因此即使点的位置完全自由，在对称分布的前提下，积分阶数的上限仍为
对于任意高阶的积分，多项式内积的精确积分是非常困难的。进一步的改进可能需要突破格点数与多项式数目相同，格点分布对称，甚至以多项式函数作为基函数等前提假设。
参考文献：
[1]Zhong H, Yu T. Flexural vibration analysis of an eccentric annular Mindlin plate [J]. Archive of Applied Mechanics, 2007, 77(4): 185―195.
[2]Bellman R, Casti J. Differential quadrature and long term integration [J]. Journal of Mathematical Analysis and Applications, 1971, 34(2): 235―238.
[3]Shuai Yuan, Hongzhi Zhong, Consolidation analysis of non-homogeneous soil by the weak form quadrature element method [J]. Computers and Geotechnics, 2014,62: 1―10.
[4]申志强, 钟宏志. 界面滑移组合梁的几何非线性求积元分析[J]. 工程力学, 2013, 30(3): 270―275.Shen Zhiqiang, Zhong Hongzhi. Geometically nonlinear quadrature element analysis of composite beams with partial interaction [J]. Engineering Mechanics, 2013,30(3): 270―275. (in Chinese)
[5]Zhang Run, Zhong Hongzhi. Weak form quadrature element analysis of geometrically exact shells [J].International Journal of Non-Linear Mechanics, 2015,71: 63―71.
[6]Zhang Run, Zhong Hongzhi. A quadrature element formulation of an energy-momentum conserving algorithm for dynamic analysis of geometrically exact beams [J]. Computers & Structures, 2016, 165: 96―106.
[7]Zhong H. Triangular differential quadrature [J].Communications in Numerical Methods in Engineering,2000, 16(6): 401―408.
[8]Zhong H, Hua Y, He Y. Localized triangular differential quadrature [J]. Numerical Methods for Partial Differential Equations, 2003, 19(5): 682―692.
[9]徐嘉, 钟宏志. 一种三角形求积元[EB]. 中国科技论文在线, http://www.paper.edu.cn/releasepaper/content/201202-150, 2012-02-08.Xu Jia, Zhong Hongzhi. A triangular quadrature element[EB]. Sciencepaper Online, http://www.paper.edu.cn/releasepaper/ content/ 201202-150, 2012-02-08. (in Chinese)
[10]Zhong H, Xu J. A non-uniform grid for triangular differential quadrature [J]. Science China Physics,Mechanics & Astronomy, 2016, 59(12): 124611.
[11]Trefethen L. Spectral methods in Matlab [M].Philadelphia: SIAM, 2000.
[12]Ciarlet P. The finite element method for elliptic problems[M]. Amsterdam, North-Holland, 1978.
[13]Helenbrook B. On the existence of explicit hp-finite element method using Gauss-Lobatto integration on the triangle [J]. SIAM Journal of Numerical Analysis, 2009,47(2): 1304―1318.
[14]Van Oosterom A, Strackee J. The solid angle of a plane triangle [J]. IEEE Transactions on Biomedical Engineering, 1983, BME-30(2): 125―126.
[15]Proriol J. Sur une famille de polynomes à deux variables orthogonaux dans un triangle [J]. Comptes Rendus Mathématique. Académie des Sciences.Paris, 1957, 245:2459―2461.
[16]Koornwinder T. Two-variable analogues of the classical orthogonal polynomials [M]// Askey R A. Theory and application of special functions. New York: Academic Press, 1975: 435―495.
[17]Lyness J, Cools R. A survey of numerical cubature over triangles [M]// Mathematics of Computation 1943-1993:a half-century of computational mathematics.Proceedings of Symposia in Applied Mathematics,American Mathematical Society, Providence, RI, 1995,48: 12―150.
[18]Zhang L, Cui T, Liu H. A set of symmetric quadrature rules on triangles and tetrahedra [J]. Journal of Computational Mathematics, 2009, 27(1): 89―96.
[19]喻畑. 二维问题的弱形式求积元分析[D]. 北京: 清华大学, 2007: 31―35.Yu Tian. Weak-form quadrature element analysis of two-dimensional problems [D]. Beijing: Tsinghua University, 2007: 31―35. (in Chinese)